Определенный интеграл

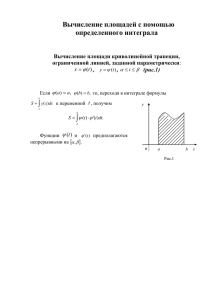
ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ
ЗАДАЧА О ВЫЧИСЛЕНИИ
ПЛОЩАДИ ПЛОСКОЙ
Решим задачу о вычислении площади фигуры,
ФИГУРЫ
ограниченной графиком функции y  f x,
отрезками прямых
,
и осью
Ox.Такую фигуру называют криволинейной
трапецией
x  a, x  b
a
xi 1 xi
b
ЗАДАЧА О ВЫЧИСЛЕНИИ ПЛОЩАДИ
ПЛОСКОЙ ФИГУРЫ
Разобьем отрезок a, b на n частей
точками a  x0 , x1, x2 ,..., xi 1, xi ,..., xn  b .
При этом криволинейная трапеция разобьется
на n элементарных криволинейных
трапеций. Заменим каждую такую
криволинейную трапецию прямоугольником с
основанием xi  xi  xi 1 , где i  1,2,.., n и

высотой h  f xi , где xi -произвольно
выбранная внутри отрезка xi 1, xi  точка.
ЗАДАЧА О ВЫЧИСЛЕНИИ ПЛОЩАДИ
ПЛОСКОЙ ФИГУРЫ
Площадь прямоугольника будет

равна Si  f xi xi , а площадь
всей криволинейной фигуры
приблизительно будет равна
сумме площадей всех
прямоугольников:
n
n
i 1
i 1

S   Si   f xi xi .
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Определение.
n

Выражение  f xi xi , где
i 1
xi  xi  xi 1 , называется
интегральной суммой функции f x 
на отрезке a, b .
Определение.
Если существует конечный
n
lim
 
 f xi xi , не
max xi 0 i 1
зависящий ни от способа разбиения отрезка
a, b на части, ни от выбора точек xi  xi1 , xi  ,
то этот предел называется определенным
интегралом функции f x  на отрезке a, b и
b
обозначается  f x dx .
a
Замечание.
С геометрической точки зрения
b
при f x   0  f x dx равен
a
площади криволинейной
трапеции
ТЕОРЕМА О СУЩЕСТВОВАНИИ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Теорема.
Если функция f x  непрерывна на
отрезке a, b , то
n
 
 f xi xi
lim
max xi 0 i 1
существует и конечен, т.е.
b
существует и конечен  f x dx .
a
СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
a
1.  f x dx  0 ;
a
b
2.  dx  b  a ;
a
b
a
3.  f x dx    f x dx ;
a
b
b
4.   f1 x   f 2 x dx   f1 x dx   f 2 x dx ;
a
b
b
a
a
СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
b
b
a
b
a
5.  Kf x dx  K  f x dx ;
c
b
a
c
6.  f x dx   f x dx   f x dx ;
a
b
7.  f x dx  0 , если f x   0 .
a
ТЕОРЕМА О СУЩЕСТВОВАНИИ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ДНЕМ
Если функция непрерывна на[ a, b],
существует такая точка
b
что
  [a, b],
 f ( x)dx  f ( )(b  a).
a
y  f (x)
a

b
то
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Теорема.
Пусть F x  - первообразная функции f x  .
b
Тогда  f x dx  F b   F a  .
a
Эту формулу называют формулой
Ньютона-Лейбница, из которой следует,
что для вычисления определенного
интеграла необходимо найти
первообразную подынтегральной функции.
ПРИМЕР
3 
Вычислить
x
3 
e 3 dx
e
0
1
3  x
e 3 dx


0
0

x
3 dx
.
1
 x
3e 3
3
0

 3 e
1

1
  1 3
 0 
 3 e 3  e 3  




1 e
1 
 1  3  1  3
e
e 
ВЫЧИСЛЕНИЕ ИНТЕГРАЛА
Теорема (Замена переменной в
определенном интеграле).
Пусть f x  непрерывна на a, b , а
функция x   t  непрерывна вместе
со своей производной  t  на
отрезке  ,   , причем a     ,
b     . Тогда
b

a

 f x dx   f  t  t dt .
ПРИМЕР
x 1  t
x 1  t 2
3

0
xdx
2 t2
 x  t  1, dx  2tdt  
1
x 1
x  0, t  1
2
1
2tdt 
t
x  3, t  2




2
t

 8
  1 


  2 t  1 dt  2  t  1 dt  2
t
 2   2     1 


  3 
1
1
 3
 3
1
2
2
2
2
3
1 
4 8
8
7 
 2  2   1  2  1  2  
3 
3 3
3
3 
Теорема (Интегрирование по
частям в определенном
интеграле).
Если функции u  ux  , v  vx  и их
производные u  x  и
v x  непрерывны на отрезке a, b , то
b
b
a
a
b
 udv  u  v   vdu .
a
ПРИМЕР
dx
e dx
u  ln x, du 
e

x  x ln x 1   x
 ln xdx 
x
1
1
dv  dx, v  x
e
 x ln
e
x1
e
  dx  e ln e  ln 1 
1
e
x1
 e  e 1  1
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
Замечание.

 f x dx не является определенным интегралом.
a
Считается по определению, что

b
 f x dx  lim  f x dx . Если этот предел
a
b  a

конечен, то  f x dx , называемый
a
несобственным, сходится.
Если же этот предел не является конечным, то
интеграл расходится.
ПРИМЕР
Вычислить несобственный интеграл


0
xdx
x2  4
(или установить его расходимость).


0
b
xdx
1
d ( x 2  4) 1
2
 lim  2
 lim ln( x  4) 
2
0
b

x 4 2
x 4
2 b
0
b
1
 lim (ln(b 2  4)  ln 4)  
2 b
Этот несобственный интеграл расходится.
ПРИМЕР
Несобственный интеграл


0
dx

2
x 4
1
b 1


 lim arctg  arctg () 

b  2
2 2
22 4
ГЕОМЕТРИЧЕСКИЕ
ПРИЛОЖЕНИЯ
ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
Площадь фигуры в декартовых
координатах.
y
y  f x 
x
0
a
b
Площадь такой
фигуры, называемой
криволинейной
трапецией,
вычисляют по
b
формуле S   f x dx .
a
ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ
Площадь фигуры, ограниченной графиками непрерывных
функций y  f 1 x  , y  f 2 x  , f 1 x   f 2 x  и двумя прямыми
b
x  a и x  b определяется по формуле S    f 2 x   f1 x dx
a
В случае параметрического задания
кривой, площадь фигуры, ограниченной
прямымиx  a, x  b, осью Ох и кривой
x   (t ), y   (t ), вычисляют по
t2
формуле S   (t ) (t )dt ,

t1
где пределы интегрирования определяют из
уравнений
a   (t1 ), b   (t 2 ).
.
Площадь полярного сектора вычисляют по
формуле

1 2
S   r ( )d
2
.
β
α
r  r ( )
ПРИМЕРЫ
Вычислить площадь фигуры, ограниченной
линиями
и
2
y  x  2x  3
y  x 2 1
Получим
S    x  2 x  3  x  1dx    2 x
1
1
2
2
2

 2 x  4 dx 
2
2
1


x
x

 2x  
 2  x 2  x  2 dx   2

3
2
2

 2
1


3
2
 1 1
8
  8 4

1 1

 2    2       4   2   2   6  
3
  3 2

3 2

 3 2
1

 9
 2 3  8    2    9
2

 2
ПРИМЕРЫ
x2 y2
Найти площадь эллипса 2  2  1.
a
b
Параметрические уравнения эллипса
x  a cos t , y  b sin t.
0
S  4  b sin t (a sin t )dt 
 /2
у
 /2
b
х
о
a
 4ab  sin tdt  4ab
2
0
 /2

0
1  cos 2t
dt 
2
1
1

 /2
 4ab(t  sin 2t ) 0  2ab  ab.
2
2
2
ПРИМЕР
Площадь фигуры, ограниченной
лемнискатой Бернулли r 2  a 2
и лежащей вне круга радиусаr
1
2
 /6
1
0 a cos 2d  2
2
 /6

0
a

2
cos 2
:
2
 /6
a
1 2
1 2
d  ( a sin 2  a  )
2
4
4
0
1 2
 
a2
3 
a2

 a (sin  ) 
(
 )
( 3 )
4
3 6
4 2
6
8
3
a2

S
2
( 3
3
)

ВЫЧИСЛЕНИЕ ДЛИНЫ ДУГИ
Если кривая задана параметрическими
y,   t , то длина ее
уравнениямиx   t
t2
дуги

l

t1

 t 2   t 2 dt
,
где t1 ,t 2 –значения параметра,
соответствующие концам дуги .
ДЛИНА ДУГИ В ДЕКАРТОВЫХ
КООРДИНАТАХ
Если bкривая задана уравнением y  f x ,
то l   1   f x 2 dx, где a, b–абсциссы начала и
a
конца
дуги a  b .
Если кривая задана
уравнением
d
x  g y , то l  c 1  g  y 2 dy , где c, d–
ординаты начала и конца дуги c  d

 



ДЛИНА ДУГИ В ПОЛЯРНЫХ
КООРДИНАТАХ
Если кривая задана уравнением в полярных
координатах      , то

l

  
2
2

    d
,
где  ,  –значения полярного угла,
соответствующие концам дуги .
ПРИМЕРЫ
Вычислить длину дуги кривой
от точки O0,0  до B 4,8 .

 
3 12


y   x   x
  2
3
2
4
l

0
9
4
1  x dx 
4
9
y x
3
, тогда
4

0
4 2 9 
  1  x 
9 3 4 
9  9 
1  xd 1  x  
4  4 
3
2
4
0


8

10 10  1
27
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
ВРАЩЕНИЯ.
Объем тела, образованного вращением вокруг
оси Ox криволинейной трапеции,
a оси
xb
ограниченной
, отрезком
y  f кривой
x
x  a , xи прямыми
b
абсцисс
,
вычисляется по формуле

b
Vx  π
  f x  dx
2
a
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
ВРАЩЕНИЯ
Объем тела, образованного вращением вокруг
оси Oy фигуры, ограниченной кривой x  g y
, отрезком оси ординат
c  y  d и прямыми y  c , y  d
, вычисляется по формуле
 
d
Vy  
.




g
y

c
2
dy
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА
ВРАЩЕНИЯ
y  x2
y
y x
1
А
0
1
Рис. 14
Искомый объем
можно найти как
разность объемов,
полученных
вращением вокруг
оси Ox
криволинейных
трапеций,
ограниченных
линиями y  x
и
2
yx
РЕШЕНИЕ
Тогда
1
  x  dx    x  dx 
1
Vx  
2
0
1
1
2
x
  xdx   x dx   
2
0
0


01
4


3
  
2 5 10
0
2 2
5 1
x
 
5
0
