opredelenniy integral

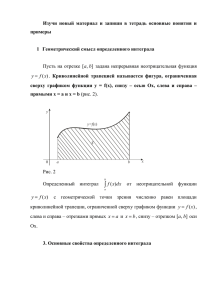
ТЕМА:
ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ
П Р Е П О Д А В АТ Е Л Ь
М АТ Е М АТ И К И : М О Р О З О В А Н . В .
Решим задачу о вычислении площади фигуры,
ограниченной графиком функции y  f x , отрезками
прямых x  a , x  b и осью Ox. Такую фигуру
называют криволинейной трапецией
a
xi 1 xi
b
ЗАДАЧА О ВЫЧИСЛЕНИИ ПЛОЩАДИ
ПЛОСКОЙ ФИГУРЫ
Разобьем отрезок a, b на n частей точками
a  x0 , x1, x2 ,..., xi 1, xi ,..., xn  b .
При этом криволинейная трапеция разобьется
на n элементарных криволинейных
трапеций. Заменим каждую такую
криволинейную трапецию прямоугольником с
основанием xi  xi  xi 1 , где i  1,2,.., n и

высотой h  f xi , где xi -произвольно
выбранная внутри отрезка xi 1, xi  точка.
ЗАДАЧА О ВЫЧИСЛЕНИИ ПЛОЩАДИ
ПЛОСКОЙ ФИГУРЫ
Площадь прямоугольника будет

равна Si  f xi xi , а площадь
всей криволинейной фигуры
приблизительно будет равна
сумме площадей всех
прямоугольников:
n
n
i 1
i 1

S   Si   f xi xi .
ЗАДАЧА О ВЫЧИСЛЕНИИ ПЛОЩАДИ
ПЛОСКОЙ ФИГУРЫ
Определение.
Если существует конечный
n
lim
 
 f xi xi , не
max xi 0 i 1
зависящий ни от способа разбиения отрезка
a, b на части, ни от выбора точек xi  xi 1 , xi  ,
то этот предел называется определенным
интегралом функции f x  на отрезке a, b и
b
обозначается  f x dx .
a
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
b

a
Для непрерывной функции
f ( x)dx  F ( x) |  F (b)  F (a)
b
a
где F(x) – первообразная функции f(x).
СВЯЗЬ МЕЖДУ ОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ И
ПЕРВООБРАЗНОЙ
(ФОРМУЛА НЬЮТОНА - ЛЕЙБНИЦА)
ПРИМЕР
x
3 
e 3 dx

x
3 
e 3 dx
0
1
3  x
e 3 dx


0
0

1
 x
3e 3
3
0

 3 e
1

1
  1 3
 0 
 3 e 3  e 3  




1 e
1 
 1  3  1  3
e
e 
a
1.  f x dx  0 ;
a
b
2.  dx  b  a ;
a
b
a
3.  f x dx    f x dx ;
a
b
b
4.   f1 x   f 2 x dx   f1 x dx   f 2 x dx ;
a
b
b
a
a
СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
b
b
a
b
a
5.  Kf x dx  K  f x dx ;
c
b
a
c
6.  f x dx   f x dx   f x dx ;
a
b
7.  f x dx  0 , если f x   0 .
a
СВОЙСТВА ОПРЕДЕЛЕННОГО
ИНТЕГРАЛА
Площадь криволинейной трапеции, ограниченной
графиком непрерывной положительной на
промежутке [a;b] функции f(x), осью x и прямыми
x=a и x=b:
b
S   f ( x)dx
a
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Площадь криволинейной
трапеции, ограниченной
графиком непрерывной
отрицательной на
промежутке [a;b] функции
f(x), осью x и прямыми
x=a и x=b:
b
S    f ( x)dx
a
Замечание: Если функция
изменяет знак на
промежутке [a;b] , то
b
S1  S 2   f ( x)dx
a
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
ОПРЕДЕЛЕННОГО ИНТЕГРАЛА