1 - Nirvana.FM
реклама
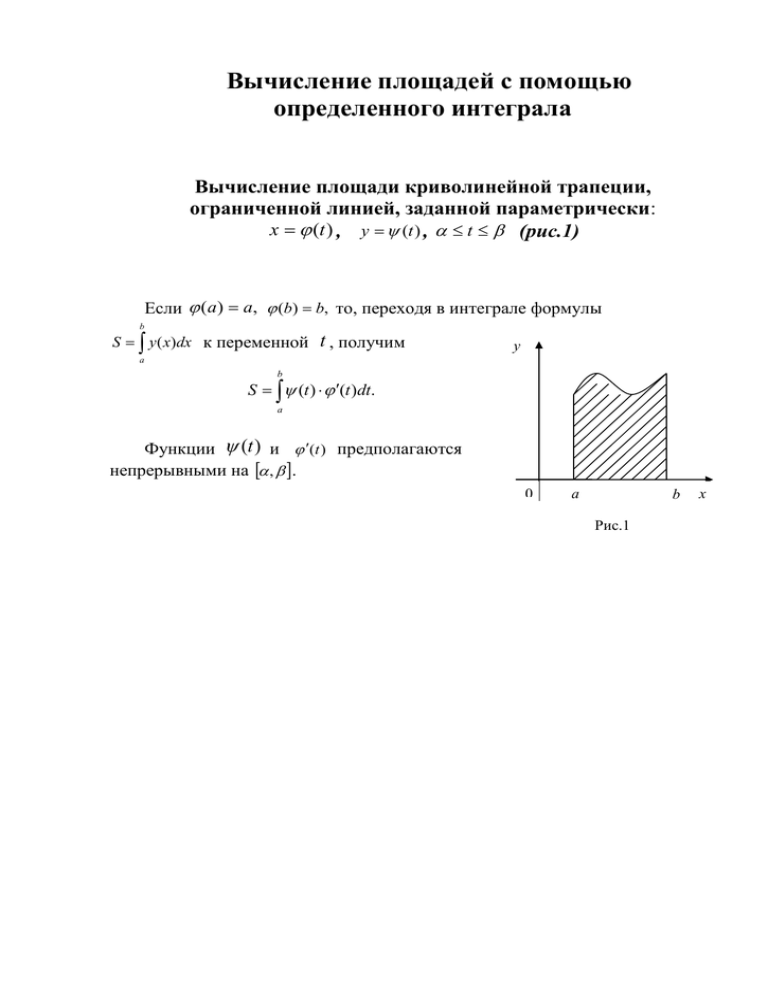
Вычисление площадей с помощью определенного интеграла Вычисление площади криволинейной трапеции, ограниченной линией, заданной параметрически: x (t ) , y (t ) , t (рис.1) Если (a ) a, (b) b, то, переходя в интеграле формулы b S y( x)dx к переменной t , получим y a b S (t ) (t )dt. a Функции (t ) и (t ) предполагаются непрерывными на , . 0 a b Рис.1 x Вычисление длин дуг плоских кривых Что понимается под длиной дуги AB (рис.2) Ai Ai+1 A1 An-1 A B Рис. 2 Впишем в AB ломанную A0 A1 A2 ... An линию (через A0 обозначена точка A, через An - точка B). Обозначим через длину наибольшего звена ломанной и рассмотрим множество всевозможный ломанных, вписанных в AB . Определение. Если при 0 существует конечный предел L периметров всевозможных ломанных, вписанных в AB , то этот предел называется длиной дуги , а сама дуга при этом называется спрямляемой. Таким образом, def L lim 0 n 1 AA i 0 i i 1 . Вычислительные формулы для длины дуги при различных способах задания кривой 1. Кривая задана уравнением y f (x), a x b . Функция f (x) непрерывна и имеет непрерывную производную f (x) на a, b : b L 1 f 2 ( x)dx . (1) a 2. Кривая задана параметрически x=x(t), y=y(t), t . Функции x(t) и y(t) непрерывны и имеют непрерывные производные на , , причем x (t ) 0 . L ( x(t )) 2 ( y (t )) 2 dt . (2) 3. Кривая задана в полярных координатах уравнением r r ( ) , . Функция r ( ) непрерывна и имеет непрерывную производную r ( ) на , : L r ( )) 2 (r ( )) 2 d . (3) Дадим краткие пояснения к выводу формул (1) - (3). n 1 b 1 f 2 (ci )xi 1. L 1 f ( x)dx lim 0 2 i 0 a К пределу аналогичной суммы придем, если воспользуемся определением длины дуги и формулой конечных приращений Лагранжа (рис.3). y Ai+1 Ai xi 0 xi yi xi+1 Рис. 3 x def L lim 0 n 1 AA i 0 i i 1 . Ai Ai 1 (xi ) 2 (yi ) 2 , где yi f ( i )xi i - некоторая точка промежутка xi , xi 1 . 2. Формулу (2) получим, если в интеграле формулы (1) перейдем к переменной t при условии, что x( ) a , x( ) b . При этом воспользуемся формулой f ( x) dy y (t ) , dx x (t ) x (t ) 0 . 3. Чтобы получить формулу (3), следует воспользоваться формулами x r cos , y r sin перехода от полярных координат к декартовым и задать кривую в виде: x r cos , y r sin , . Полученные соотношения можно рассматривать как параметрические с параметром уравнения кривой. Останется убедиться, что ( x( )) 2 r 2 ( ) r 2 ( ) , и воспользоваться формулой (2). Вычисление работы с помощью определенного интеграла Пусть под действием некоторой силы F материальная точка M движется по прямой Os, причем направление силы совпадает с направлением движения. Требуется найти работу, произведенную силой F при перемещении точки M из положения s = a в положение s = b. 1) Если сила F постоянна, то работа A выражается произведением силы F на длину пути, т.е. A = F(b-a). 2) Предположим, что сила F непрерывно меняется в зависимости от положения материальной точки, т.е. представляет собой функцию F(s), непрерывную на отрезке a s b. Разобьем отрезок a, b на n произвольных частей с длинами s1 , s 2 ,..., s n , затем в каждом частичной отрезке si 1 , si выберем произвольную точку i и заменим работу силы F(s) на пути si произведением F ( i )si . Это значит, что в пределах каждого частичного отрезка мы принимаем силу F за постоянную, а именно полагаем F = F ( i ) . В таком случае выражение F ( i )si при достаточно малом si дает нам приближенное значение работы силы F на пути si , а сумма n An F ( i )si i 1 будет приближенным выражением работы силы F на всем отрезке a, b . Очевидно, An представляет собой интегральную сумму, составленную для функции F = F(s) на отрезкке a, b . Предел этой суммы при max( si ) 0 существует и выражает работу силы F(s) на пути от точки s = a до точки s = b: b A F ( s)ds . a Объем тела вращения Рассмотрим тело, образованное вращением вокруг оси Ox криволинейной трапеции aABb, ограниченной кривой y = f(x), осью Ox и прямыми x = a, x = b. В этом случае произвольное сечение тела плоскостью, перпендикулярной к оси абсцисс, есть круг, площадь которого 2 Q y 2 f (x) . Применяя общую формулу для вычисления объема b Q( x)dx , a получим формулу для вычисления объема тела вращения: b b y dx f ( x)2 dx . 2 a a y x y a xa (e e x a ) 2 Рис. 4 Пример. Найти объем тела, образуемого вращением цепной линии y a xa (e e x a ) 2 Вокруг оси Ox на участке от x = a до x = b (рис. 4) Решение. b a2 a 2 a 2 a 2 x a a 2 x a 2x a 2 x a (e x a e x a ) 2 dx ( e 2 e ) dx e 2 x e 4 0 4 0 4 2 2 0 b a 3 8 (e 2b a b e 2b a ) a 2 b 2 .








![Приложение 1 [презентация]](http://s1.studylib.ru/store/data/004787532_1-bc289a17fd4cb5810b33d06c20138199-300x300.png)