Определенный интеграл и его приложения

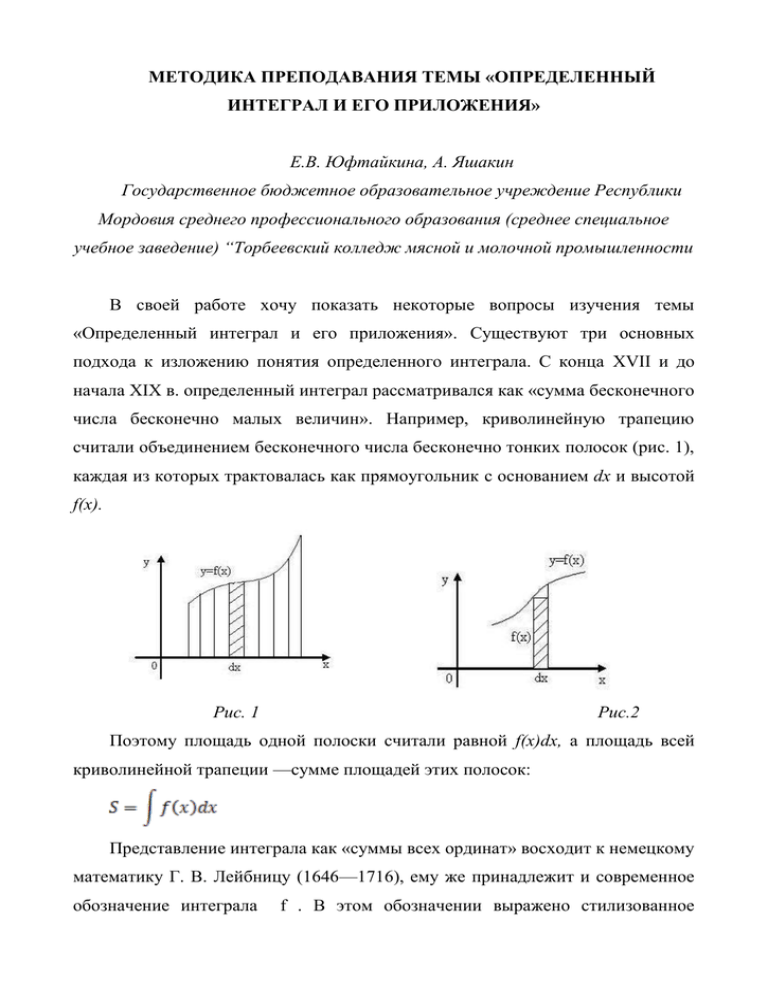
МЕТОДИКА ПРЕПОДАВАНИЯ ТЕМЫ «ОПРЕДЕЛЕННЫЙ
ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ»
Е.В. Юфтайкина, А. Яшакин
Государственное бюджетное образовательное учреждение Республики
Мордовия среднего профессионального образования (среднее специальное
учебное заведение) “Торбеевский колледж мясной и молочной промышленности
В своей работе хочу показать некоторые вопросы изучения темы
«Определенный интеграл и его приложения». Существуют три основных
подхода к изложению понятия определенного интеграла. С конца XVII и до
начала XIX в. определенный интеграл рассматривался как «сумма бесконечного
числа бесконечно малых величин». Например, криволинейную трапецию
считали объединением бесконечного числа бесконечно тонких полосок (рис. 1),
каждая из которых трактовалась как прямоугольник с основанием dx и высотой
f(x).
Рис. 1
Рис.2
Поэтому площадь одной полоски считали равной f(x)dx, а площадь всей
криволинейной трапеции —сумме площадей этих полосок:
Представление интеграла как «суммы всех ординат» восходит к немецкому
математику Г. В. Лейбницу (1646—1716), ему же принадлежит и современное
обозначение интеграла
f . В этом обозначении выражено стилизованное
изображение первой буквы слова summa. Название «интеграл» принадлежит
ученику Лейбница швейцарскому математику Я. Бернулли (1654—1705).
Этот подход, используемый и сегодня во многих физических задачах, не
выдерживает критики с точки зрения математической строгости, так как фраза
«бесконечно тонкая полоска» не имеет точного смысла: если ширина полосок
равна нулю, то, поскольку сумма нулей равна нулю, и площадь всей
криволинейной трапеции равна нулю, а если ширина полосок отлична от нуля,
то нельзя отождествлять такую полоску с прямоугольником — она, хоть и
немного, но отличается от прямоугольника (рис. 2).
От французского математика О. Коши (1789—1857) ведет свое начало
второй подход к изложению понятия определенного интеграла, когда отрезок
[а, Ь] разбивают на части точками:
Т : а = х0 < х1 < х2 < . .. < xn-1 < хп =b, в каждом отрезке [хr, xr+1] (r = 0, 1, 2,
..., n—1) берут произвольную точку 𝜉r (xr 𝜉r Xr+1) и образуют сумму
ST=f (𝜉0)(x1 - х0) + f (𝜉1) (х2-х1) + f (𝜉n-1)(xn-xn-1)
Эта сумма зависит от выбора точек xr и 𝜉r. Но, как показал Коши в 1823 г.,
если функция( y=f(x) непрерывна на [а, Ь], то суммы Sт, получающиеся при
различном выборе точек Xr и 𝜉r, стремятся к вполне определенному пределу
(интегралу), когда максимальная из разностей (хr—Xr-1) (называемая обычно
диаметром разбиения Т пли мелкостью разбиения Т) стремится к нулю:
Здесь
— мелкость разбиения, а
Как мы уже отмечали, Коши применял свое определение интеграла только
к непрерывным функциям. Определить интеграл
как предел,
содержащийся в правой части равенства во всех тех случаях, когда этот предел
однозначно определен, предложил в 1853 г. немецкий математик Б. Риман
(1826—1866). Оказалось, что интегрируемы в смысле Римана не только
непрерывные на отрезке [а, b] функции; класс интегрируемых функций более
широк, он содержит, в частности, ограниченные разрывные функции, имеющие
конечное или счетное множество точек разрыва.
Следует, однако, заметить, что предел в равенстве (1) понимается в особом
смысле; он означает, что для любого
>0 найдется такое δ>0, что для любого
разбиения, имеющего мелкость, меньшую δ, и любого выбора точек 𝜉r [xr;xr+1]
выполняется неравенство
Этот предел не является ни пределом последовательности, ни пределом
функции, а потому применимость к нему основных свойств пределов требует
особого доказательства. Это является серьезным методическим препятствием.
Студенты с трудом усваивают громоздкую запись интегральной суммы, не
вполне понимают доказательства, в которых используются эти суммы, в
частности доказательства свойств определенного интеграла. Следует также
отметить, что при выводе, например, свойства интеграла от суммы, мы
опираемся на то, что предел суммы равен сумме пределов, т. е. идем на
сознательный обман студентов, аппелируя к факту, которого они не знают
(ведь, повторим, применимость к рассматриваемым пределам теорем о
пределах последовательностей или функций не доказывается).
Остановимся, наконец, на третьем подходе к введению понятия
определенного интеграла, при котором определенным интегралом называется
разность значений первообразной на концах рассматриваемого отрезка. При
таком подходе формула Ньютона — Лейбница не доказывается, а принимается
за исходный пункт всей теории. Ясно, что такой путь возможен лишь в тех
случаях, когда известна первообразная для подынтегральной функции или
известен хотя бы сам факт существования этой первообразной.
В заключение заметим, что, на наш взгляд, в методическом арсенале
преподавателя должны быть все три подхода: первый даст возможность
преподавателю получить ряд важных физических результатов, второй —
проводить математические рассуждения с достаточной строгостью, третий —
достаточно быстро и без особых усилий довести до учащихся основные
положения теории определенного интеграла.