Учитель: Щуракова Л.А. с. Б. Сорокино 2009г.
реклама

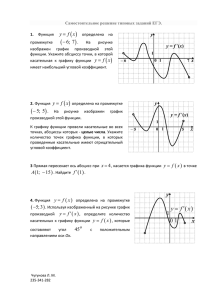
Учитель: Щуракова Л.А. с. Б. Сорокино 2009г. 1) Вступление. 2) Алгоритмы для решения заданий с производной. 3) Задания А-части в тестах ЕГЭ. 4) Задания В-части в тестах ЕГЭ. 5) Задания С-части в тестах ЕГЭ. Задания, где требуется применение производной функции наиболее часто встречаются в Едином Государственном Экзамене. Это задания А-части (нахождение производной и её физический смысл), задания B-части (графики с использованием производной, нахождение наибольшего и наименьшего значений функции) и задания C-части (задания с развернутым ответом, при решении которых необходимо использовать производную функции). Поэтому, мы считаем, что наш слайд поможет выпускникам успешного выполнить подобные задания на ЕГЭ. Алгоритм монотонности функции: 1) Находим область определения (D). 2) Находим производную функции. 3) Находим стационарные точки (f ’(x)=0). 4) Методом интервалов устанавливаем промежутки знаков постоянства производной. 5) Если на промежутке f ’(x)>0, то функция возрастает на данном промежутке. Если на промежутке f ’(x)<0, то функция убывает на данном промежутке. Алгоритм нахождения точек экстремума: 1) Находим область определения (D). 2) Находим производную функции. 3) Находим стационарные точки (f ’(x)=0). 4) Методом интервалов устанавливаем промежутки знаков постоянства производной. 5) Если при переходе через производная меняет знак с “+” на “-”, то это точка max, если наоборот, то точка min. Алгоритм нахождения наибольшего и наименьшего значений функции на отрезке : 1) Найти значения функции на концах отрезка, т. е. числа f (a) и f (b). 2) Найти её значения в тех критических точках, которые принадлежат интервалу (a; b). 3) Из найденных значений выбрать наибольшее и (или) наименьшее. 1) Найти момент остановки тела, движущегося по закону Решение. О т в е т: 3. 2) Найдите производную функции . 3) Точка движется по координатной прямой согласно закону , где – координата точки в момент времени t. В какой момент времени скорость точки будет равна 5? 4) Найдите производную функции 5) Через точку графика функции у = ех – с абсциссой х0 = 1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс. 6) При движении тела по прямой расстояние S ( в метрах) от начальной точки движения изменяется по закону S(t) = (t – время движения в секундах). Найдите скорость (м/с) тела через 4 секунды после начала движения. . 1) Функция y = f (x) определена на промежутке (-3;7). На рисунке изображен график её производной. Найдите точку x0, в которой функция y = f (x) принимает наименьшее значение. Решение. На промежутке (-3;3) производная функции y = f (x) отрицательна, и эта функция непрерывна на промежутке (3;3], следовательно, данная функция убывает на промежутке (3;3]. С другой стороны, на промежутке (3;7) производная функции y = f (x) положительна, и эта функция непрерывна на промежутке [3;7), следовательно, данная функция возрастает на промежутке [3;7). Таким образом, свое наименьшее значение функция y = f (x) принимает в точке x0 = 3. 2) При каком наименьшем натуральном значении n уравнение ровно один корень? Решение. Запишем данное уравнение в виде Рассмотрим функции и . Построим схематически график функции D(y1)=R. имеет . Рис. 1 Очевидно, что уравнение имеет единственное решение, если –n>175 или -n<-81, то есть n<-175 или n>81. Наименьшее натуральное значение n равно 82 (рис. 2). О т в е т: 82. 3) Функция у = f(x) определена на промежутке (– 6; 4). График ее производной изображен на рисунке. Укажите точку минимума функции у = f(x) на этом промежутке. у у = f (x) 1 –6 4) Найдите наибольшее целое значение функции 1 4 . 5) Найдите наименьший корень уравнения 6) Найдите наименьшее значение функции 0 . . Примечание. Не всегда задания на нахождение наибольшего и наименьшего значений функции нуждаются в применении производной, так как их проще решить при помощи анализа данной функции. х 1) Найдите значение функции Решение. 1. Найдем область определения функции в точке максимума. : Упростим формулу, задающую функцию: 2. , при ( x = 1 не принадлежит области определения функции f). x = - 1 – точка максимума f (-1) = 2. О т в е т: 2. 2) Для монтажа оборудования необходима подставка объемом 1296 дм3 в форме прямоугольного параллелепипеда. Квадратное основание подставки будет вмонтировано в пол, а ее задняя стенка – в стену цеха. Для соединения подставки по ребрам, не вмонтированным в пол или стену, используется сварка. Определите размеры подставки, при которых общая длина сварочного шва будет наименьшей. Решение. 1. В основании подставки лежит квадрат. Пусть x – длина его стороны, а y – и , т. е. . высота подставки. Тогда ее объем равен 2. Сварить надо 3 ребра верхнего основания и 2 ребра грани, параллельной стене. Значит, общая длина L сварки равна 3x + 2y, т. е. , . 3. Найдем производную Поэтому . , т.е. функция L (x) при x > 0 имеет единственную критическую точку x = 12 . и L’(x) < 0. Если x > 12 , то и 4. Если 0 < x < 12, то Значит, x = 12 является точкой минимума и О т в е т: 12 дм, 12 дм и 9 дм. . . Тогда высота подставки равна 3) Стороны прямоугольника равны 2 и 5. Через каждую точку на его меньшей стороне провели прямую, отсекающую прямоугольный треугольник с периметром 8. Найдите наименьшее значение площади оставшейся части прямоугольника. 4) Найдите наибольшее значение функции . 5) Требуется разметить на земле участок АСDЕGНМN площадью 1200м2, состоящий из трех прямоугольных частей и имеющий форму, изображенную на рисунке, где ЕG = 30 м, НМ = 5 м, МN = 20 м и DЕ >= 10 м. Найдите наименьшее значение периметра такого участка и какие-либо значения длин КL, АL и DE, при которых периметр является наименьшим. 6) Для монтажа оборудования необходима подставка объемом 162 дм3 в форме прямоугольного параллелепипеда. Квадратное основание подставки будет вмонтировано в пол, а ее задняя стенка — в стену цеха. Для соединения подставки по ребрам, не вмонтированным в пол или стену, используется сварка. Определите размеры подставки, при которых общая длина сварочного шва будет наименьшей.