    y

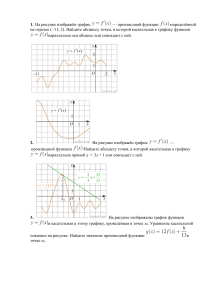
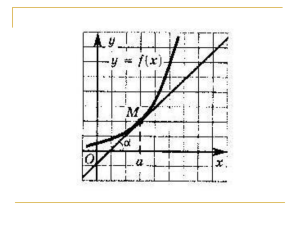
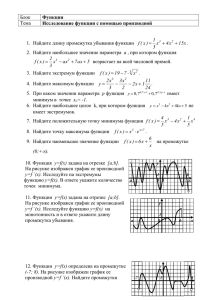
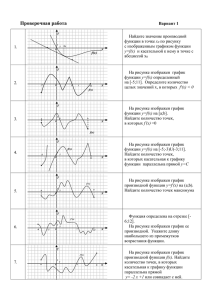
Самостоятельное решение типовых заданий ЕГЭ.
1.
y  f  x  определена на
  6; 7  . На рисунке
Функция
промежутке
y
y = f (x)
изображен график производной этой
функции. Укажите абсциссу точки, в которой
касательная к графику функции
y  f  x
1
6
7 x
0 1
имеет наибольший угловой коэффициент.
2. Функция
  5; 5 .
y  f  x  определена на промежутке
На
рисунке
изображен
y
график
y = f (x)
производной этой функции.
1
К графику функции провели касательные во всех
точках, абсциссы которых - целые числа. Укажите
количество точек графика функции, в которых
проведенные касательные имеют отрицательный
угловой коэффициент.
5
0 1
5
x
3 Прямая пересекает ось абсцисс при x  4 , касается графика функции y  f  x  в точке
A 1;  15  . Найдите f  1 .
4. Функция y  f  x  определена на промежутке
 5; 3  . Используя изображенный на рисунке график
производной y  f   x  , определите количество
касательных к графику функции y  f  x  , которые
составляют
угол
направлением оси Ox.
Чугунова Л. М.
235-341-282
45
o
с
положительным
y
1
y  f  x 
01
x
5. Функция y  f  x  определена на промежутке
  3; 6  .
производной
На
рисунке
y  f  x  .
изображен
Определите
график
y  f  x 
число
касательных к графику функции y  f  x  , тангенс
угла
наклона
которых
к
положительному
направлению оси Ox равен 3.
Чугунова Л. М.
235-341-282
y
1
0 1
x