Приложение 6. Производная функции в задачах
реклама

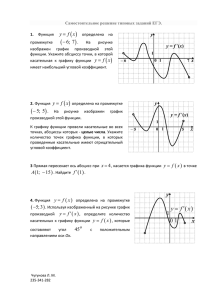
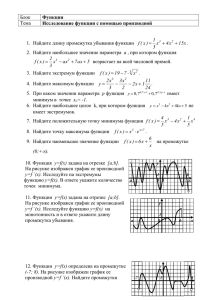
Приложение 6. Производная функции в задачах Пример 1. Построить график функции f ( x ) = х4 - 2х2 - 3 Решение: 1. D(f)=R. 2. четная 3.а) вертикальных асимптот нет б) lim(x4 -2х2 -3) = . 4. точки пересечения с осями а) с ОХ: у=0, x = ± 3 б) с OY: х=0, у=3 5. f ' ( x ) = 4 x 3 - 4 x . f ' ( x ) = 0 . x = 1 , - 1 . x f'(x) f (x) (-;-1) -1 (-1;0) 0 (0;1) 1 (1;+) 0 0 - 0 + -4(min) -3(max) -4(min) Для построения графика функции полезно сначала на координатной плоскости отметить точки (-1;-4), касательные (0;-3), к (1;-4), графику учитывая, функции в что этих экстремальных точках параллельны оси ОХ. Потом, используя данные таблицы, нужно «написать» ход кривой в точках экстремума. Построение самого графика явится завершающим этапом и не вызовет затруднений. Отработать навыки построения кривой в окрестности точки в зависимости от значения производной функции в этой точке надо заранее, до построения графика функции. Я начинаю формировать этот навык с момента изучения материала о геометрическом смысле производной. В работе я сталкиваюсь с проблемой, что дети не всегда могут сопоставить график функции и график производной. Полезными являются такие типы задач: 1. Изобразите кривую, касающуюся прямых, заданных на рисунке, в отмеченных точках: 2.Укажите, в каких точках функция, заданная графически, не имеет производной; имеет производную; имеет производную, равную нулю Y X Изобразите график такой функции, которая в двух точках не имеет производную, а в трех точках ее производная обращается в ноль. Изобразите график такой функции, которая непрерывна на всей числовой оси и имеет: а) две точки максимума и одну точку минимума; б) две точки максимума и три точки минимума; в) две точки максимума и ни одной точки минимума. Предполагаемая система упражнений направлена на то, чтобы учащиеся не допускали ошибки следующего рода: 1) график функции f ( x ) = х 3 - 2 х 2 + х должен быть 2) функция f ( x ) = x 2 - x 4 должна иметь график, А ученики ошибочно строят другие эскизы графиков. Эти ошибки происходят из-за того, что при построении графиков функций берут во внимание лишь характер монотонности функции и то, какой экстремум имеет функция в той или иной экстремальной точке, забывая при этом учесть существует ли при этом производная функции в этих точках. График функции f ( x ) = x 2 – х 4 построен так, что в точках с абсциссами х= 1 2 и х= - 1 2 к кривой нельзя провести касательных, в то время как производная функции в этих точках существует. В работе я сталкиваюсь с проблемой, что дети не могут сопоставить график функции и график производной. Поэтому на уроках я предлагаю учащимся задачи следующего типа. Пример 2. На рисунке изображен график производной функции y = f ' ( x ) , заданной на отрезке [-2; 10]. Исследуйте функцию y=f(x) на монотонность и укажите длину промежутка возрастания. Пример 3. Функция y=f(x), определена на промежутке (-3;7). График ее производной изображен на рисунке. Укажите число точек минимума функции y=f(x) на промежутке (-3;7). Пример 4. Функция y = f ( x ) , определена на промежутке (-4;3). График ее производной изображен на рисунке. Укажите число точек максимума функции y=f(x)на промежутке (4;3). Пример 5. Функция y = f ( x ) , определена на промежутке (-6;4). График ее производной изображен на рисунке. Укажите число точек минимума функции y=f(x)на промежутке (6;4). Пример 6. Функция y = f ( x ) , определена на промежутке (-5;7). График ее производной изображен на рисунке. Найдите промежутки убывания функции y=f(x). В ответе укажите наибольшую из длин этих промежутков.