1 + i - Euroakadeemia

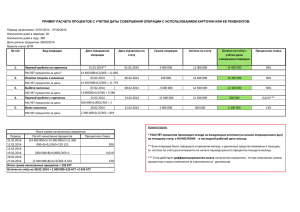
ЛЕКЦИЯ 4.
ОСНОВЫ ФИНАНСОВОЙ МАТЕМАТИКИ
Natalja Viilmann, PhD
КРАТКИЙ ПЛАН ЛЕКЦИИ:
 Типы
задач на проценты
 Проценты в банковской сфере
 Простые и сложные проценты
ПРИМЕНЕНИЕ СХЕМЫ СЛОЖНЫХ
ПРОЦЕНТОВ ЦЕЛЕСООБРАЗНО В ТЕХ
СЛУЧАЯХ, КОГДА:

проценты не выплачиваются по мере их начисления, а
присоединяются к первоначальной сумме долга.
Присоединение начисленных процентов к сумме долга,
которая служит базой для их начисления, называется
капитализацией процентов;

срок ссуды более года.
Сложные проценты характеризуют процесс роста
первоначальной суммы со стабильными темпами
роста, при наращении ее по абсолютной
величине с ускорением, следовательно, формулу
сложных процентов можно рассматривать как
определение уровня на базе стабильных темпов
роста.


цепной темп роста равен:
(1 + i)
базисный темп роста за весь период, исходя из
постоянного темпа прироста, имеет вид:
(1  i)
n
НАРАЩЕНИЕ
ПО ПРОСТЫМ И СЛОЖНЫМ ПРОЦЕНТАМ
Простейшим видом финансовой операции являет-ся
однократное предоставление в долг некоторой суммы PV (present
value) с условием, что через некоторое вре-мя t будет возвращена
большая сумма FV (future value).
6
Результативность подобной сделки может быть
оценена различными показателями:
7
FV 
1  d 
8
FV 
PV
n
PV
m
 d
 1 
m




nm

Прямая задача предполагает суммарную
оценку наращенного денежного потока, т.е. в
его основе лежит будущая стоимость.
FV  P1  r 
n

Обратная задача предполагает суммарную
оценку дисконтированного (приведенного)
денежного потока.
PV 
Fn
1  r 
n
ЗАДАЧА 1.
Найдите будущую стоимость FV 1 000 $,
инвестированных на 2 года под 11,8% по
схеме начисления сложных процентов.
FVt = PV (1 + r)t = 1000 (1 + 0,118)2 =
1000×1,2499 = 1249,90 $
ЗАДАЧА 2
Найдите будущую стоимость FV 770 $,
инвестированных на 1,5 года под 9,8% по
схеме начисления сложных процентов
каждые полгода.
FVt = PV (1 + r/m)tm = 770 (1 + 0,098/2)1,5×2 =
770×1,1543 = 888,81 $.
ЗАДАЧА 3.
Вычислите приведенную стоимость PV 1759 $,
которые предполагается получить через 2
года, если сложная ставка процентов
составляет 12,9%.
PV = FVt/(1 + r)t = 1759/(1 + 0,129)2 = 1759/1,2746
= 1380,04 $
ЗАДАЧА 5.
Если будущая стоимость FV 830 руб.,
вложенных на 2 года, составляет 950 р.,
какова ставка сложных процентов?
 FV 
 950 
i%=  t
-1  100%=  2
-1  100%=7,0%
 PV 
 830 
ЗАДАЧА №7. УСЛОВИЯ
Предположим, вы сегодня положили на счет 1000р., и на
эту сумму ежегодно начисляются 8%.
1) Сколько денег вы будете иметь через 4 года?
2) Сколько денег вы будете иметь, если деньги
начисляются ежеквартально?
ЗАДАЧА №7.РЕШЕНИЕ
1)
Будущая стоимость 1000 р. при 8% через 4 года
FV = PV(1+i)t = 1000×(1+0,08)4 = 1000×1,36049 = 1360,49 (р.)
Если 8% начисляются ежеквартально, то ежеквартальная ставка
равна 8%/4квартала = 2% в квартал. Через 4 года, т.е. через 16
кварталов, получаем следующий результат
FV = PV(1+i)t = 1000×(1+0,02)16 = 1000×1,37279 = 1372,79 (р.)
Отметим, что мы можем посчитать эту величину следующим образом:
EAR = (1 + 0,08/4)4 – 1 = 1,024 – 1 = 0,08243,
EAR (Equivalent Annual Rate) – эффективная годовая ставка процентов,
которая дает тот же результат что m-разовое начисление процентов
по номинальной ставке.
Коэффициент капитализации (множитель наращения - (1+i)t) был бы
равен
(1 + 0,08243)4 = 1,37277
В результате мы приходим к такому же результату.
2)
ЗАДАЧА 8.
Предположим, вы только что отпраздновали ваш 19-й день
рождения. Богатый дядюшка основал для вас
инвестиционный фонд, по которому по достижении 25
лет вы получите 100 000$. Если соответствующая
учетная ставка равна 11%, то сколько этот фонд стоит
сегодня?
Современная (приведенная) стоимость инвестиционного
фонда равна
PV = FV/(1+i)t = 100000/(1+0,11)6 = 100000/1,87041 = 53464 $
ЗАДАЧА №9. УСЛОВИЯ ЗАДАЧИ
Первый отобранный в первом раунде футбольных игр
защитник получает трехлетний контракт на 10млн.р.
Игрок сразу получает бонус размере 1млн.р. Затем
получает в качестве зарплаты 2млн.р. в конце первого
года, затем 3млн.р. в конце следующего года и 4млн.р. в
конце последнего года.
Предположим, что учетная ставка 10% годовых.
Стоит ли данный контракт 10 млн.?
Сколько стоит данный контракт сегодня?
ЗАДАЧА №9. РЕШЕНИЕ
Для решения данной задачи воспользуемся формулой:
n
FV 3
FV t
FV1
FV 2
FV n
PV 


 ... 

1
2
3
n
t
(1  i)
(1  i)
(1  i)
(1  i)
(1

i)
t 1
Подставляя данные задачи в формулу, получаем
PV = 1/(1+0,1)0 + 2/(1+0,1)1 + 3/(1+0,1)2 + 4/(1+0,1)3 =
= 1 + 2/1,1 + 3/1,21 + 4/1,331 =
= 1 + 1,81818181 + 2,47933884 + 3,00525920 =
= 8,30277985 (млн.р.) = 8 302 779,85 р.
ЗАДАЧА №10. УСЛОВИЯ ЗАДАЧИ
Вы планируете вложить несколько сумм на счет с
начислением процентов.
Сегодня вы депонируете 1000р., 2000р. через 2 года и
8000р. через 5 лет.
Вы снимаете со счета 3000р. через 3 года и 5000р. через 7
лет.
1) Сколько вы будете иметь через 8 лет при ставке 9%,
т.е. чему равна FV через 8 лет при ставке 9%?
2) Чему равна PV этих денежных потоков?
ЗАДАЧА №10. РЕШЕНИЕ
IF, OF, р.
Приведенный ниже график помогает разобраться с
движением денежных потоков при ответе на первый вопрос.
FV
+1000
×
(1 + 0,09)8
0
+2000
×
(1 + 0,09)6
+8000
×
(1 + 0,09)3
8
1
2
3
-3000
×
(1 + 0,09)5
4
5
6
7
-5000
×
(1 + 0,09)1
t,
лет
ВОПРОСЫ?