Четвертое задание - kurchatov1189.ru

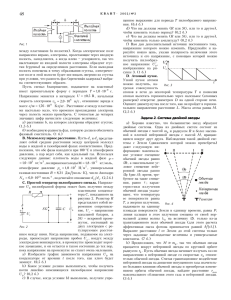
Äîìàøíåå çàäàíèå ïî ñòåðåîìåòðèè  4
Çàäà÷à 1
 ÷åòûðåõóãîëüíîé ïèðàìèäå P ABCD âñå ðåáðà ðàâíû
√
2.
1. ×åìó ðàâíî ðàññòîÿíèå ìåæäó ñåðåäèíîé ðåáðà P B è ñåðåäèíîé ðåáðà AD?
2. Ïóñòü òî÷êà K ëåæèò íà ðåáðå P B , à òî÷êà L ëåæèò íà ðåáðå AD. P K = DL = x. Âûðàçèòå
KL êàê ôóíêöèþ îò x.
3. Â êàêèõ ãðàíèöàõ ëåæèò KL?
4. Ïóñòü òî÷êà K äâèæåòñÿ ïî ëîìàíîé P BCP , à òî÷êà L äâèæåòñÿ ïî ëîìàíîé DAP D. Äâèæåíèå íà÷àòî îäíîâðåìåííî è èäåò ñ îäíîé ñêîðîñòüþ.  êàêèõ ãðàíèöàõ ëåæèò KL?
Çàäà÷à 2
 ÷åòûðåõóãîëüíîé ïèðàìèäå P ABCD îñíîâàíèåì ÿâëÿåòñÿ êâàäðàò ABCD, ãðàíü P BC ðàâíîáåäðåííûé òðåóãîëüíèê (P B = P C ), ïåðïåíäèêóëÿðíûé îñíîâàíèþ. AD = 2, ðàññòîÿíèå îò P
äî îñíîâàíèÿ ðàâíî 1. Òî÷êà K ñåðåäèíà ðåáðà P A; òî÷êà L ñåðåäèíà ðåáðà CD, òî÷êà Q ñåðåäèíà ðåáðà BC .
1. Âû÷èñëèòå ðàññòîÿíèÿ:
à) KL; á) îò òî÷êè Q äî ïëîñêîñòè P AD; â) îò ïðÿìîé CD äî ïëîñêîñòè P AB ; ã) îò ïðÿìîé
AB äî äî ïðÿìîé P D; ä) îò B äî òðåóãîëüíèêà P AC .
2. Åñòü ëè òî÷êà, êîòîðàÿ ðàâíîóäàëåíà îò âñåõ:
à) âåðøèí ïèðàìèäû; á) ïëîñêîñòåé ãðàíåé ïèðàìèäû?
Çàäà÷à 3
ABCDA1 B1 C1 D1 ïðÿìîóãîëüíûé ïàðàëëåëåïèïåä. AD = 1, DC = 3, AA1 = 2.
1. Íàéäèòå óãîë ìåæäó ïðÿìûìè A1 D è D1 C .
2. Ìîæåò ëè óãîë ìåæäó ïðÿìûìè D1 X1 è AC ðàâíÿòüñÿ 30◦ ? (Òî÷êà X1 ëåæèò íà ðåáðå B1 C1 .)
3. Íàéäèòå óãîë α ìåæäó ïðÿìûìè B1 D è AC .
4.  êàêèõ ãðàíèöàõ ëåæèò óãîë β ìåæäó ïðÿìûìè AA1 è DX2 , ãäå òî÷êà X2 íàõîäèòñÿ íà
ëîìàíîé A1 B1 C1 ?
5. Òî÷êà K ëåæèò íà ðåáðå D1 D, òî÷êà L ëåæèò íà ðåáðå CC1 , D1 K = CL. Îïðåäåëèòå âèä óãëà
ìåæäó ëó÷àìè AK è DL.
Çàäà÷à 4
 ïðÿìîóãîëüíîì ïàðàëëåëåïèïåäå ABCDA1 B1 C1 D1 : AB = 1, AD = 2, AA1 = 1.
1. Íàéäèòå óãëû, êîòîðûå îáðàçóåò äèàãîíàëü ïàðàëëåëåïèïåäà ñ åãî ãðàíÿìè.
2. Íàéäèòå óãëû, êîòîðûå îáðàçóåò äèàãîíàëü B1 D ñ äèàãîíàëüíûìè ïëîñêîñòÿìè.
3. Ïóñòü òî÷êà K äâèæåòñÿ ïî ðåáðó BC îò B ê C . Êàê èçìåíÿåòñÿ óãîë ìåæäó äèàãîíàëüþ
BD1 è ïëîñêîñòüþ AB1 K ?
Çàäà÷à 5
 ïðàâèëüíîé ïðèçìå ABCA1 B1 C1 âñå ðåáðà ðàâíû 1.
1. Íàéäèòå óãëû, êîòîðûå ïëîñêîñòü A1 C1 B îáðàçóåò ñ áîêîâûìè ãðàíÿìè ïðèçìû.
2. ×åìó ðàâåí áîëüøèé äâóãðàííûé óãîë ìåæäó ïëîñêîñòÿìè A1 C1 B è B1 C1 A?
3. Ïóñòü òî÷êà K äâèæåòñÿ ïî ðåáðó AA1 îò A ê A1 , à òî÷êà L äâèæåòñÿ ïî ðåáðó BB1 îò B
ê B1 . Äâèæåíèå íà÷àòî îäíîâðåìåííî è èäåò ñ îäíîé ñêîðîñòüþ. Êàê èçìåíÿåòñÿ óãîë ìåæäó
ïëîñêîñòÿìè A1 C1 L è B1 C1 K ?
Çàäà÷à 6
 òðåõãðàííîì óãëå ñ âåðøèíîé O è ëó÷àìè a, b, c:
ïðîâåäåí ëó÷ Ox. Ïóñòü 6 xa = 6 xb = α.
6
ca = 6 cb = 90◦ ,
6
ab = 60◦ . Âíóòðè óãëà
1. ×åìó ðàâåí óãîë ϕ ìåæäó ëó÷àìè x è c?
2. Ìîæåò ëè 6 xc = α?
3. ×åìó ðàâåí óãîë ìåæäó ëó÷îì b è ïëîñêîñòüþ, ïðîõîäÿùåé ÷åðåç ëó÷è c è x?
4. Óñòàíîâèòå âèä äâóãðàííîãî óãëà ñ ðåáðîì x, îäíà ãðàíü êîòîðîãî ïðîõîäèò ÷åðåç ëó÷ a, à
äðóãàÿ ÷åðåç ëó÷ b.