Задачи 4 тура 2011/2012 года Задача 1. Функция = ( )определена
реклама
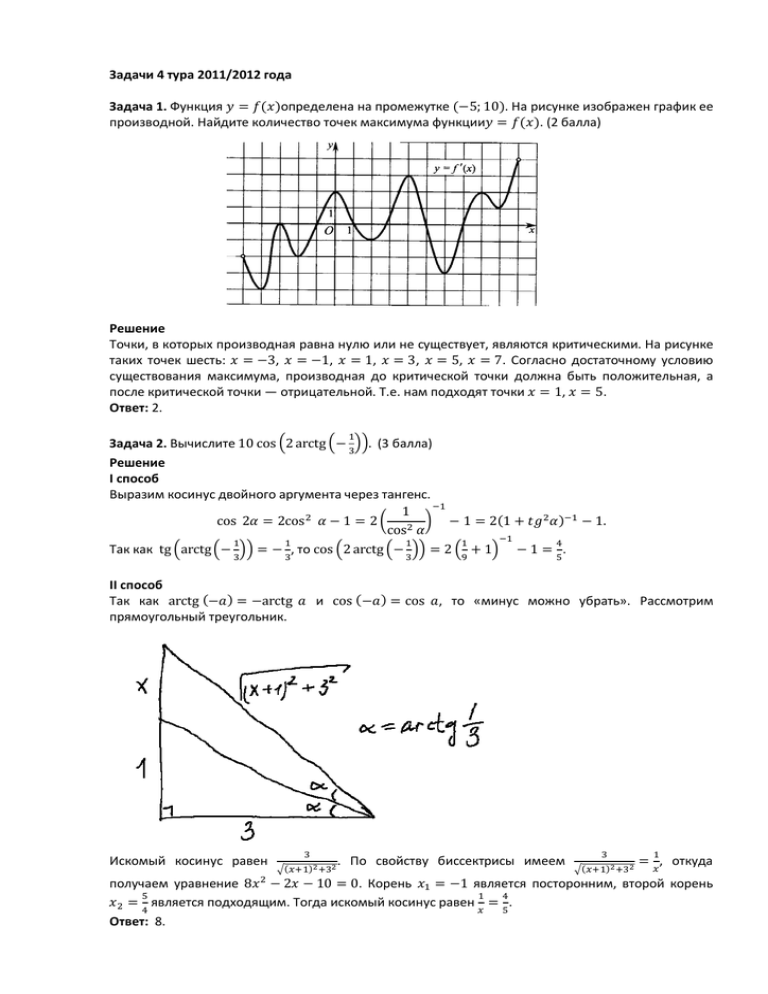
Задачи 4 тура 2011/2012 года Задача 1. Функция = ( )определена на промежутке (−5; 10). На рисунке изображен график ее производной. Найдите количество точек максимума функции = ( ). (2 балла) Решение Точки, в которых производная равна нулю или не существует, являются критическими. На рисунке таких точек шесть: = −3, = −1, = 1, = 3, = 5, = 7. Согласно достаточному условию существования максимума, производная до критической точки должна быть положительная, а после критической точки — отрицательной. Т.е. нам подходят точки = 1, = 5. Ответ: 2. Задача 2. Вычислите 10 cos 2 arctg − . (3 балла) Решение I способ Выразим косинус двойного аргумента через тангенс. 1 cos 2 = 2cos −1= 2 cos Так как tg arctg − = − , то cos 2 arctg − II способ Так как arctg (− ) = −arctg прямоугольный треугольник. Искомый косинус равен ( − 1 = 2(1 + =2 +1 ) − 1. −1= . и cos (− ) = cos , то «минус можно убрать». Рассмотрим ) . По свойству биссектрисы имеем ( ) = , откуда получаем уравнение 8 − 2 − 10 = 0. Корень = −1 является посторонним, второй корень = является подходящим. Тогда искомый косинус равен = . Ответ: 8. Задача 3. Решите уравнение 2 ⋅3 ⋅7 = 504 . (5 баллов) Решение 2 ⋅3 ⋅7 = 504 ⇔2 ⋅3 ⋅7 = (2 ⋅ 3 ⋅ 7) = 1 ⇔ 42 = 42 ⇔ 2 − 6 = 0 ⇔ = 3. Ответ: 3. ⇔2 ⋅3 ⋅7 Задача 4. Найдите количество натуральных значений аргумента из промежутков убывания функции = log , . (5 баллов) Решение Построим последовательно эскизы графиков функций = log = log | | = log 2 | | 5 = log 2 | | 5 = log 2 | − 4| 5 Промежутками убывания функции являются (−∞; 1,5) и (4; 6,5]. Натуральными числами из этих промежутков являются 1, 5 и 6. Ответ: 3. Задача 5. Точки , , расположены соответственно на сторонах так, что : = 3: 1, : = 5: 1, : = 3: 5. Отрезки и Найдите отношение . (9 баллов) Решение Обозначим через точку пересечения прямых и . Применим к треугольнику теорему Менелая: ⋅ Применим к треугольнику ⋅ =1⇒ =3⋅ , , треугольника пересекаются в точке . . теорему Менелая: ⋅ ⋅ =1⇒ = Следовательно, = 12 ⇒ =3⋅ 5 8 + ⇒ 3 5 = . 3 12 + 3 + 5 ⇒ 4. 12 + 3 Ответ: 4. Задача 6. Найдите значение параметра , при котором график функции = (2 − ) + ( + 3 ) + − 4 симметричен относительно прямой = 10. (6 баллов) Решение Выделим 2 + полный + 14 является прямая Ответ: −20. − квадрат: (2 − ) + ( + 3 ) + −4= 2 +2 + 14 −4= − 4. Из свойства параболы вытекает, что осью симметрии параболы = − . Таким образом, = −20.









