уравнение tg x=a

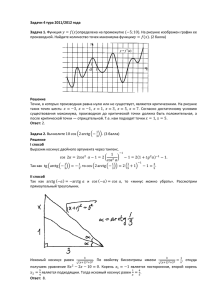
Уравнение
10 класс
tg x  a
df : tg x  a
Задача 1:
а
tg x  3
Решить уравнение:
МР  ОР
3
РОМ :
М₁
х1 
х₁
х₂
М₂
МО
М
О
Р
х2 

3
х
3
; РМ  3
;
М1, М 2
РМ
3


 3  tg х1 , х1 
РО
1
3
 2k , где k  1,  2, ...


 n, n  Z
  32k , где k  1,  2, ...
Решить уравнение: tg
Задача 2:
x  3
МР  ОР
МО
РОМ 
М₂
х1  
О
х₂
х₁
Р

3
3
М
;

3
М1, М 2
, т.е. х1  

3
 2k , где k  1,  2,...
  (2k  1), где k  1,  2,...
х
М₁
 3
х2  

; РМ  3

3
 n, n  Z


2
x

2

tg x  3  x 
3
tg x   3  x  
tg x  a a  R на интервале 


3
x
2
имеет только один корень.

a  0 корень в промежутке [0; )
2
a  0, то в промежутке (

2
;0].

2
И этот корень называется арктангенсом числа и обозначают:
arctg a
Арктангенсом числаа  R называется такое
  


число   2 ; 2  , тангенс которого равен а:






arctg a=α, если tg α=а и 2
.
2
Например:
arctg 1 

4
, так как tg

4
1 и 

2



4


2
.

3

3
 
 


arctg  
  , так как tg    и    .

6
3
2
6 2
 6
 3 
tg x  a, где a  R
x  arctg a  n, n  Z
Задача 3
arctg (a)  arctg a