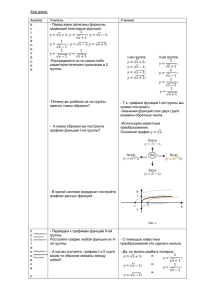
Как построить график функции y=mf(x)

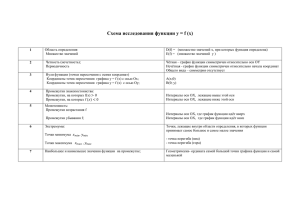
Приложение 2
Урок алгебры и начала анализа - 10 класс (Составитель – Струкова Н.Ф.)
Тип урока: интегрированный урок
 урок формирования новых знаний, проводится в форме урокаисследования.
Тема урока: Как построить график функции y=mf(x), если известен график функции
y=f(x)
Цели урока:
Образовательные цели:
 Экспериментальным путем с использованием компьютера получить алгоритм
построения графиков функции y=mf(x) по заданному графику y=f(x)
 Научиться применять полученный алгоритм для решения подобных задач без ЭВМ
Развивающие цели:
 Формирование умений анализировать, обобщать полученные результаты,
проводить исследования на компьютере в специальных программах
 Развитие самостоятельности в учебной деятельности.
Оборудование и материалы:
 Компьютеры с операционной системой Windows XP.
 Учебное электронное пособие Дрофа-ДОС для НФПК «Математика 5-11»
 Шаблоны системы координат индивидуальные у каждого ученика
 Планшеты, на которых нанесена система координат.
Ход урока:
I. Актуализация опорных знаний:
Задание 1. Построить на доске по точкам графики функций y=sin x, y=cos x
и перечислить их свойства по плану:
 Область определения функции
 Четность(нечетность) функции
 Промежутки монотонности
 Ограничения функции снизу и сверху
 Наибольшее и наименьшее значения функции в соответствующих точках
 Свойство непрерывности
 Область значений функции
(у доски работают два ученика)
Задание 2. В этой же системе координат построить графики функций


y=sin(x- ), y=cos(x+ )и перечислить их свойства по тому же плану.
3
4
( у доски работают два ученика)
Задание 3. В этой же системе координат построить графики функций


y=sin(x- )+1, y=cos(x+ )-2 и перечислить их свойства по тому же плану.
3
4
(у доски работают два ученика)
Работа анализируется всеми учащимися и оценивается учителем.
II. Организация осознания и восприятия нового материала:
Вводное слово учителя: « Вы уже знаете, как строить графики функций вида
y=sin(x+m)+n (y=cos(x+m)+n).
А знаем ли мы способ построения графиков функций y=msinx ( y=mcosx)?
Как вы думаете, изменится график функции y=f(x), если f(x) умножить на m.
Выдвигается гипотеза, как правило, верная.
Учитель: Давайте вашу гипотезу проверим. Но построение таких графиков по точкам
процесс трудоемкий, шаблон нам тоже не поможет. Поэтому мы сегодня поучимся
строить такие графики с помощью компьютера.
Итак, тема урока: «Как построить график функции y=mf(x), если известен
график функции y=f(x)»
Наша задача на уроке экспериментальным путем получить алгоритм для построения
графиков функций вида y= mf(x) или y= mf(x), где f(x)=sinx или f(x)=cosx.
Моделировать вы будете в виртуальной лаборатории Nfpk, знакомой вам с 9 класса,
где мы учились строить графики квадратичной функции.
Организация работы:
Учащиеся объединяются в пары для работы за машиной: один, выполняет роль
оператора, другой - выполняет роль аналитика-эксперта.
В ходе работы учащиеся делают записи в таблице на листе с практической работой,
анализируют полученные результаты и составляют алгоритм для решения подобных задач
в безмашинном варианте.
По окончании работы ребята объединяются в группы и обсуждают составленный
алгоритм, вносят поправки, затем от каждой группы выступает эксперт и предлагает свой
вариант алгоритма.
Практическая работа:
Как построить график функции y=mf(x), если известен график функции y=f(x), где
f(x)=sinx или f(x)=cosx.
Задание: задавая различные значения для m, кроме m=0, построить графики функций
f(x)=msinx или f(x)=mcosx. Исследовать полученные результаты и составить алгоритм
построения графиков функции вида f(x)=msinx или f(x)=mcosx без компьютера.
m
2
1
2
-1
-2
-
1
2
Формула функции
Преобразование графика
График функции__________ получается из графика
функции ________в результате __________от оси _____
С коэффициентом_______
График функции__________ получается из графика
функции ________в результате __________от оси _____
С коэффициентом_______
1. График функции__________ получается из графика
функции ________в результате __________от оси _____
с коэффициентом_______
2.
подвергнем
график
функции
________преобразованию
___________относительно
оси______
1. График функции__________ получается из графика
функции ________в результате __________от оси _____
с коэффициентом_______
2.
подвергнем
график
функции
________преобразованию
___________относительно
оси______
1. График функции__________ получается из графика
функции ________в результате __________от оси _____
с коэффициентом_______
2.
подвергнем
________преобразованию
оси______
график
функции
___________относительно
После анализа учитель предлагает вниманию учеников готовый алгоритм на
плакате.
1. Построить график основной функции y=sinx или y=cosx (его изображаем
пунктирной линией)
2. Осуществить растяжение построенного графика от оси OX с
коэффициентом m, если m>1 и осуществить сжатие к оси OX, если
1
0<m<1с коэффициентом
(полученный график изображаем тонкой
m
линией), сохраняя точки пересечения с осью OX
3. Если m<0, дополнительно подвергнуть график функции преобразованию
симметрии относительно оси OX (полученный график изобразить
сплошной жирной линией)
III. Первичное закрепление полученных знаний:
Учитель: «Теперь наша задача, научиться применять полученный алгоритм для
решения задач без компьютера. Вам предлагается поэтапно выполнить задание»
. Организация работы:
У доски работают 4 ученика по очереди, остальные ученики работают в тетрадях.
Задания 1 уровня: с помощью полученного алгоритма в системе координат построить
2
поэтапно графики функций y=3sinx, y=-3sinx, y=1,5cosx, y=sinx по готовому
3
шаблону(приложение 1), созданному в графическом редакторе Paint на интерактивной
доске, используя разноцветные электронные маркеры, объясняя подробно каждое
действие :
Первый ученик строит график функции
y= 3sinx
Второй ученик строит график функции
y= =-3sinx
Третий ученик строит график функции
y =1,5cosx
2
Четвертый ученик строит график функции y= - sinx
3
Организация работы для учащихся 2 уровня: (работа в парах)
Учащиеся выполняют работу на специальных заранее заготовленных планшетах с
нанесенной системой координат.(приложение 2) или на компьютере в графическом
редакторе Paint(приложение 2)
По окончании работы группа демонстрирует результат работы, решение обсуждается,
идет анализ ошибок с привлечением учащихся, выполнявших работу 1 уровня.
Задания 2 уровня для сильных учеников: № 235(в,г), № 236(в,г), 238(а) из задачника
Особое внимание обратить на построение графика функции под № 238(а) и на то, что

функция претерпевает разрыв в точке
2
Решение:


3 sin x, еслиx  2
F ( x)  
3x 3 , еслиx  

2
IV. Возвращение к ожидаемым результатам:
Учитель: Сейчас вам предстоит выполнить небольшой тест, результаты которого
покажут, насколько вы усвоили материал сегодняшнего урока и определят задачи
следующих уроков.
Тест
Задание:
Определите, какая графическая модель, соответствует каждой из данных
функций.
Буквы, обозначающие графики, запишите рядом с формулой.(тест прилагается)
Если работа выполнена правильно, то вы прочтете имя ученого математика, который
содействовал развитию аналитической теории тригонометрических функций.
По окончании работы условие проецируются на экран, решение каждой задачи
обсуждается, учащиеся исправляют ошибки, если таковые допущены.
Л
Э
Е
Р
Й
1
Y= sinx
3
Э
Код:
1
Y= sinx+1
2
Й
Y= - 3sinx
Л
Y=3sinx
Е
Y = 2sin(x-

3
)
Р
Сообщение о Л. Эйлере подготовлено заранее одним из учеников.(сопровождается WEB
–страницей)(приложение 3)
Развитию аналитической теории тригонометрических функций содействовали Исаак
Ньютон и Леонард Эйлер. Основоположником этой теории следует считать Л. Эйлера.
Он придал всей тригонометрии современный вид.
Дальнейшее развитие теории было предложено в XIX веке Н.И. Лобачевским и
другими учеными. В наше время тригонометрия больше не рассматривается как
самостоятельная ветвь математики.
Важнейшая ее часть - учение о тригонометричесих функциях - является частью
более общего, построенного с единой точки зрения учения о функциях, изучаемых в
математическом анализе; другая же часть - решение треугольников - рассматривается как
глава геометрии (плоской и сферической)
Дополнительное задание: построить график функции y=2sinx+3 в табличном
процессоре Excel.(работа оценивается)
V. Итог урока:
Ребята, как вы считаете, обладает ли алгоритм, который вы составили свойством
массовости?
Можно ли его использовать для построения графиков функций y=mtgx(y=mctgx)и
других функций?
Мы с вами попробуем это осуществить на одном из последующих уроков.
VI. Домашнее задание:
Домашняя самостоятельная работа на 4 варианта по карточкам.
Вариант 1.

1.Постройте график функции y=3sin(x- ).
6
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
1. Известно, что f(x) = - 0,5sinx. Найдите 4 f(-x).
Вариант 2.
1.Постройте график функции y= 2cosx+1.
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
2. Известно, что f(x) = 1,5cosx. Найдите 2 f(2x).
Вариант 3.
1.Постройте график функции y= - 0,5cos(x+

3
).
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.

2. Известно, что f(x) = 2,5sinx. Найдите 0,4 f( -x).
2
Вариант 4.
1.Постройте график функции y=-2,5sinx – 0,5
По графику найдите:
А) область значений функции;
Б) промежутки возрастания, убывания функции.
1 3
2. Известно, что f(x) = -3cosx. Найдите f(
+x).
3 2
VII. Рефлексия:
Учитель: если урок оказался для вас полезным и интересным, то оставьте на парте
кружок красного цвета, в противном случае ничего не оставляйте.
Приложение 1.
Приложение 2
(приложение 3)
Развитию аналитической теории
содействовали И.Ньютон и Л. Эйлер.
тригонометрических
функций
Основоположником этой теории следует считать Л. Эйлера.
Он придал всей тригонометрии современный вид.
Дальнейшее развитие теории было предложено в XIX веке Н.И.
Лобачевским и другими учеными.
В наше время тригонометрия больше не рассматривается как
самостоятельная ветвь математики.
Важнейшая ее часть - учение о тригонометричесих функциях - является
частью более общего, построенного
с единой точки зрения учения о функциях, изучаемых в математическом
анализе;
другая же часть - решение треугольников - рассматривается как глава
геометрии (плоской и сферической)