Схема исследования функции y = f (x)

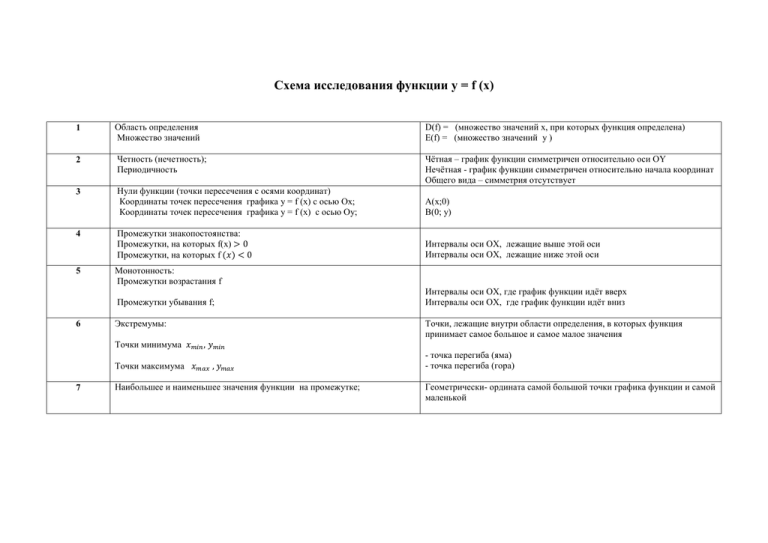
Схема исследования функции y = f (x)
1
Область определения
Множество значений
D(f) = (множество значений x, при которых функция определена)
E(f) = (множество значений y )
2
Четность (нечетность);
Периодичность
Чётная – график функции симметричен относительно оси ОY
Нечётная - график функции симметричен относительно начала координат
Общего вида – симметрия отсутствует
3
Нули функции (точки пересечения с осями координат)
Координаты точек переcечения графика y = f (x) с осью Ох;
Координаты точек пересечения графика y = f (x) с осью Оу;
А(x;0)
В(0; y)
Промежутки знакопостоянства:
Промежутки, на которых f(x) > 0
Промежутки, на которых f (𝑥) < 0
Интервалы оси OX, лежащие выше этой оси
Интервалы оси OX, лежащие ниже этой оси
4
5
Монотонность:
Промежутки возрастания f
Промежутки убывания f;
6
Экстремумы:
Точки минимума 𝑥𝑚𝑖𝑛 , 𝑦𝑚𝑖𝑛
Точки максимума 𝑥𝑚𝑎𝑥 , 𝑦𝑚𝑎𝑥
7
Наибольшее и наименьшее значения функции на промежутке;
Интервалы оси OX, где график функции идёт вверх
Интервалы оси OX, где график функции идёт вниз
Точки, лежащие внутри области определения, в которых функция
принимает самое большое и самое малое значения
- точка перегиба (яма)
- точка перегиба (гора)
Геометрически- ордината самой большой точки графика функции и самой
маленькой