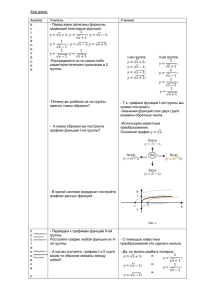
графики функций с модулем
реклама

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №4 ИМЕНИ В. БУРОВА ЭЛЕКТИВНЫЙ КУРС ПРЕДПРОФИЛЬНОГО ОБУЧЕНИЯ ( 9 КЛАСС) Ершова Т.В. (графики функций с модулем ) 10 часов г. Бежецк 2008г. Пояснительная записка Элективный курс предназначен для предпрофильной подготовки учащихся 9-хклассов общеобразовательной школы. Он расширяет и углубляет базовую программу по математике, не нарушая её целостности. Свободное владение техникой построения графиков часто помогает решать многие задачи и порой является единственным средством их решения. В основной школе представление о модуле учащиеся получают, но строить графики функций с модулем, как правило, не умеют. В 10-11 классах при решении заданий с параметром очень часто приходится рассматривать и строить такие графики. В связи с этим этот курс ориентирован на развитие у учащихся навыков построения графиков функций с модулем. Цели и задачи курса: Научить строить графики функций вида: у = | f(x)| ; y = f(| x|) и зависимостей вида |y| = f(x); |y| = | f(x);… Привлечь внимание учащихся к эстетической стороне данного вида деятельности; Показать красоту этих графиков; Развивать творческие способности учащихся. Планируемые результаты: По окончании изучения курса учащиеся должны: Знать алгоритмы построения графиков функций и зависимостей с модулем; Уметь строить графики таких функций и зависимостей; Занятия включают в себя теоретическую и практическую части—лекции, консультации, практикумы, самостоятельную и творческую работы. Итоговый контроль предусматривает выполнение творческого задания и его презентация. Формы работы: лекционная, групповая, практикум. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН № 1 2 3 4 5 6 тема занятия часы Определение модуля. Свойства и график функции у = | х | 1 График функции у = | f(х)| 1 График функции у = f(| х |) 1 График зависимости | у | = f(х) 1 График зависимости | у | = | f(х) | 1 Построение графиков функций и зависимостей более 2 сложного вида 7 Практикум 2 8 Презентация творческих работ. Организация вернисажа – 1 графики, построенные учащимися. Рекомендуемая литература А.М. и Л.Д. Назаренко " Тысяча и один пример" 1994г. А.И. Громов, В.М. Савчин " Математика для поступающих в ВУЗы" 1997г. М.А. Иванов " Математика без репетитора" –М. ВЕнтана-Граф 2002г. Я.С. Фельдман, А.Я. Жаржевский "Математика. Решение задач с модулями"— СПб. Оракул 1997г. "Математика " приложение к газете "Математика в школе" журнал Содержание и рекомендации по проведению занятий. Тема 1. Определение модуля. Свойства и график функции у = |х| Рассмотреть теоретический материал. Построение графиков функций рассмотреть двумя способами: 1. используя определение модуля; 2. применяя сдвиг графика вдоль оси ОХ, вдоль оси ОУ, растяжение, сжатие. Примеры для решения в классе и дома: у = |х| + 2; у = - | х |; у = | х| -3; у = 3|х|; у = - 0,4| х | у = |х – 1 |; у = - | х + 2 |; у = |х + 1| - 1; у = 4 - | х – 2 | Тема 2. График функции у = | f( х)| f ( x), f ( x) 0, По определению модуля: у = f ( x), f ( x) 0. Правило Для построения графика функции у = | f(х)| для всех х из области определения, надо ту часть графика функции у = f(х), которая расположена ниже оси ОХ, отобразить симметрично этой оси. Таким образом, график функции у = | f(х)| расположен только выше оси ОХ. План построения: построить график функции у = f(х) часть графика, которая располагается выше оси ОХ, остаётся без изменений; часть графика, которая расположена ниже оси ОХ , симметрично отображается относительно этой оси. 1 Примеры: построить графики а) у = |х2 + 2х -3|; б) у = | х2 -2х -3|; в) у = ; х 1 1 ; г) у = 3 ; д) у = е) у = х 1. х2 х Тема 3. График функции у = f( | х | ) f ( x), x 0, По определению модуля: у = f ( x), x 0. Правило Функция у = f(| х|) –чётная, поэтому для построения её графика достаточно построить график функции у = f( х ) для всех х 0 из области определения и отобразить построенную часть симметрично оси ОУ. План построения: построить график функции у = f(х); выделить ту часть графика, которая расположена правее оси ОУ, т.е. на множестве х > 0; выделенную часть симметрично отобразить относительно оси ОУ. 1 Примеры: построить графики а) у = х2 + 2| х | - 3; б) у = х2 -2| х | - 3; в) у = ; х г) у = ж) у = - х; х; д) у = - х2 -2| х | +3; з) у = е) у = - х2 +2|х| +3; х 1 . Тема 4. график зависимости | у | = f( х ) Эту зависимость можно записать так у = ± f( х ) Правило. Для построения графика этой зависимости достаточно построить график функции у = f( х ) для тех х из области определения, при которых f( х ) 0, и отобразить её симметрично относительно оси ОХ. План построения: построить график функции у = f( х ); выделить ту часть графика, для которой у 0; выделенную часть графика отобразить симметрично относительно оси ОХ. Примеры: построить графики а) | у | = х 2 + 2х – 3; б) | у | = - ( х2 + 2х – 3); в) | у| = 1 1 ; д) | у | = 3 ; х х ж) | у | = х 1 3 ; з) | у | = 2 – х. г) | у | = е) | у| = 1 ; х 1 3; х Тема 5. График зависимости | у | = | f( х )| Используя свойство модуля, получаем: у = f(х) и у = - f(х). Значит, графиком этой зависимости будет объединение двух графиков у = f(х) и у = - f(х). План построения: построить график у = f(х); построить график у = - f(х). Примеры: построить графики а) | у | = | х |; б) | у – 4 | = | х + 2 |; в) | у| = | 2х – х 2 |; 1 г) | у | = ; д) | у| = х 3 . х Тема 6. Построение графиков функций и зависимостей более сложного вида Примеры: построить графики 1. у = | х 2- 2 | х| - 3 |; 2. у = | - х 2 + 6 х – 8 |; 3. у = | | х – 1 | - 1 |; 4. у = | | 1 – х | + 1 |; 5. | у + 1 | = 2 – х; 6. | у | = х + 4; 7. | х | + | у | = 2; 8. | у | - | х | = 3; 9. у = | | | х | - 2 | - 1 |. Тема 7. Практикум Учащиеся разбиваются на группы по 2-3 человека. Каждая группа получает своё задание, которое выполняет самостоятельно. Выполнив её, они отчитываются перед всеми о своей работе. На этом занятии каждый ученик получает творческое задание, которое выполняет дома и готовит презентацию. Графики функций или зависимостей ученики строят на отдельном листе крупным планом, чтобы можно было организовать выставку-вернисаж этих работ. Задания для практикума: построить график 1. | х | + | у | = 2; 2. у = | х – 3 | .( х + 1 ); 3. | | х | - | у | | = 1; 4. у = | х + 1 | + | х – 2 |; 2 5. у = ; 6. | у | = х 2 – 4 |х | + 3. х 1 1 Творческие задания: построить график 1. | у | = х 2 + 4х + 3; 2. у + | у | = х; 3. у = | 2 х 1 |; 4. у = х .| у |; 5. у = | 2 - х 1 |; 6. у = | 2| х | - 4 | - | 2х + 3 |; 7. у = | 2 - 3 х |; 9. у = | 3х – 2 | - 3| х + 1 |; 11. | у | = 2| х | - 4 ; 14. у = | 2х + 4 | - 2| х – 3 |; 8. у = | 2 - х 3 ; 10. | у | = 4 – х ; 12. у = х 2 х ; 14. у = | 3х +2 | - | 3 |х| - 3 |.