Лосицкая Н.А. - Методы построения графиков функций

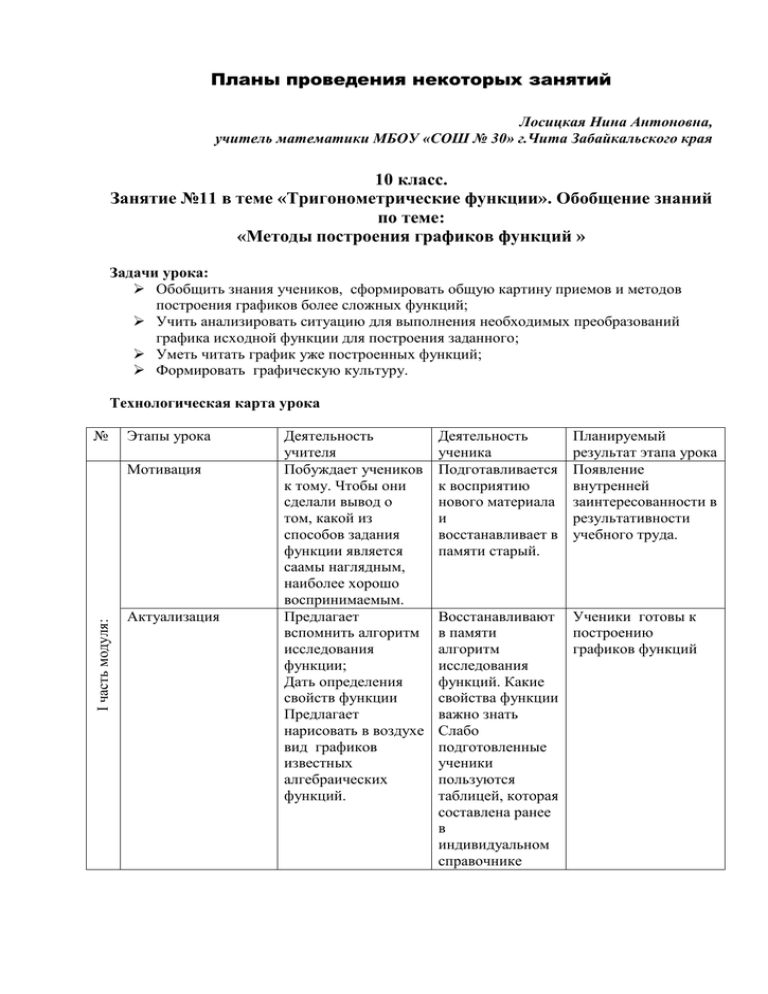
Планы проведения некоторых занятий
Лосицкая Нина Антоновна,
учитель математики МБОУ «СОШ № 30» г.Чита Забайкальского края
10 класс.
Занятие №11 в теме «Тригонометрические функции». Обобщение знаний
по теме:
«Методы построения графиков функций »
Задачи урока:
 Обобщить знания учеников, сформировать общую картину приемов и методов
построения графиков более сложных функций;
 Учить анализировать ситуацию для выполнения необходимых преобразований
графика исходной функции для построения заданного;
 Уметь читать график уже построенных функций;
 Формировать графическую культуру.
Технологическая карта урока
№
Этапы урока
I часть модуля:
Мотивация
Актуализация
Деятельность
учителя
Побуждает учеников
к тому. Чтобы они
сделали вывод о
том, какой из
способов задания
функции является
саамы наглядным,
наиболее хорошо
воспринимаемым.
Предлагает
вспомнить алгоритм
исследования
функции;
Дать определения
свойств функции
Предлагает
нарисовать в воздухе
вид графиков
известных
алгебраических
функций.
Деятельность
ученика
Подготавливается
к восприятию
нового материала
и
восстанавливает в
памяти старый.
Планируемый
результат этапа урока
Появление
внутренней
заинтересованности в
результативности
учебного труда.
Восстанавливают Ученики готовы к
в памяти
построению
алгоритм
графиков функций
исследования
функций. Какие
свойства функции
важно знать
Слабо
подготовленные
ученики
пользуются
таблицей, которая
составлена ранее
в
индивидуальном
справочнике
II часть модуля:
Обобщение знаний
по методам
построения графиков
функций.
III часть модуля:
Контроль знаний
Подача домашнего
задания
Организует
мыслительную
деятельность
учеников всех
уровней
подготовленности к
восприятию методов
построения
графиков более
сложных функций.
Эвристическая
беседа
сопровождается
демонстрацией
медиапрезентации,
на слайдах которой
представлены
графики известных
алгебраических
функций и
рассматриваются
приемы построения
графиков
тригонометрических
функций.
Предлагает решить
самостоятельную
работу.
Называют
необходимые
преобразования
графика
известной
функции, для
того чтобы
построить график
заданной
функции.
Заполняют таблицу с
правилами
построения и видами
преобразований
графиков функций.
Выбирают
уровень задания,
решают
уравнения,
подбирая для
решения
рациональный
метод.
Предлагает
подборку
тригонометрических
уравнений,
различных по
уровню и методам
решения.
Выбирает
уровень
домашней работы
Самостоятельное
применение знаний
по рациональному
использованию
методов решения
тригонометрических
уравнений.
Реализация учебнопознавательной
задачи, поставленной
на урок.
Закрепление знаний
приемов и методов
решения
тригонометрических
уравнений.
1. Мотивация: известно, что функцию можно задать несколькими способами. Из всех
способов задания функции наибольшие возможности для применения аппарата
математического анализа дает аналитический способ, а наибольшей наглядностью
обладает графический. Вот почему математический анализ основывается на глубоком
синтезе аналитических и геометрических методов. Исследование функций, заданных
аналитически, проводится гораздо легче и становится наглядным, если параллельно
рассматривать и графики этих функций. Чтобы убедиться, достаточно вспомнить
исследование квадратных уравнений, решение неравенство второй степени с одним
неизвестным при помощи исследования графиков квадратных трехчленов; исследование
систем двух уравнений первой степени с двумя переменными при помощи рассмотрения
возможных случаев взаимного расположения двух прямых на плоскости.
2. Актуализация знаний:
Что значит изучить заданную функцию?
Какими элементами характеризуется поведение функции?
Дайте определение этих элементов:
Область определения функции;
Область значений функции;
Четность;
периодичность;
нули функции;
точки разрыва;
промежутки знакопостоянства;
интервалы монотонности;
экстремумы;
асимптоты.
Формирование новых знаний проводится в форме эвристической беседы. Используется
при этом компьютер. На доске с помощью медиапроектора демонстрируются слайды, на
которых представлены различные преобразования графиков функций. Одновременно на
одном слайде представлены преобразования алгебраической функции y=x2и
тригонометрической y=sinx.
В ходе эвристической беседы в тетрадях учеников возникает сводная таблица:
3. Методы построения графиков функций
Функция
Y=f(x)+a
Y=f(x+a)
Правило построения функции данного вида
Для того, чтобы построить график функции
Y=f(x)+a, надо график функции Y=f(x)
сдвинуть вдоль оси ординат на а единиц (с
учетом знака а)
Для того, чтобы построить график функции
Y=f(x+a) надо график функции Y=f(x)
сдвинуть вдоль оси абсцисс на а единиц (с
учетом знака а)
График
4
3
2
1
0
-1
-2
4
3
2
1
0
-1
-2
Y=f(x+n)+m
Y=-f(x)
Для того, чтобы построить график функции
Y=f(x+a) +m, надо график функции Y=f(x)
сдвинуть вдоль оси абсцисс на «-а» единиц
и вдоль оси ординат на «m» единиц (с
учетом знаков m и n)
Для того, чтобы построить график функции
Y=-f(x), надо построить график,
симметричный графику функции Y=f(x)
относительно оси абсцисс.
4
3
2
1
0
-1
-2
4
3
2
1
0
-1
-2
Y=f(-x)
Для того, чтобы построить график функции
4
3
1
0
-1
-2
Y=-f(x), надо построить график,
симметричный графику функции Y=f(x)
относительно оси ординат..
Для того, чтобы построить график функции
Y=Af(x), надо ординаты всех точек графика
функции Y=f(x) увеличить по абсолютной
величине в А раз , если А>1 и уменьшить в
А раз, если 0<A<1
Y=f(nx)
Для того, чтобы построить график функции
Y=f(nx), (n>0) надо абсциссы всех точек
графика функции Y=f(x) уменьшить по
абсолютной величине в n раз , если n>1 и
увеличить в n раз, если 0<n<1
Y=Af(nx+k)+m Для того, чтобы построить график функции
 
k 
Y=Af(nx+k)+m=Ff n x    m , надо:
n 
 
1. Ординаты всех точек графика Y=f(x)
изменить в А раз.
2. абсциссы всех точек полученного
графика изменить в nраз;
3. сдвинуть полученный график вдоль
k
оси абсцисс на - ;
т
4. сдвинуть полученный график вдоль
оси ординат на m.
Для
того,
чтобы построить график функции
Y=f( x )
Y=f( x ) надо:
1. поострить график функции Y=f(x)
при f(x)  0,
2. достроить график симметрично
полученному графику относительно
оси ординат
Для того, чтобы построить график функции
Y= f (x)
Y= f (x) , надо оставить без изменения те
участки графика Y=f(x), где f(x)  0, и
построить изображения, симметричные
графику функции Y=f(x) относительно оси
абсцисс на тех участках, где f(x)<0
Y=Af(x)
4
3
1
0
-1
-2
4
3
1
0
-1
-2
4
3
1
0
-1
-2
4
3
2
1
0
-1
-2
4
3
2
1
0
-1
-2
Задание для работы с помощью консультантов или учителя (сложность задания
выбирает ученик):
А) Постройте график функции y=-1,5cosx
1

В) Постройте график функции y=3sin( х  )
2
6
1

С) Постройте график функции y= - 5sin( х  )
2
4
4
5. Самостоятельная работа: