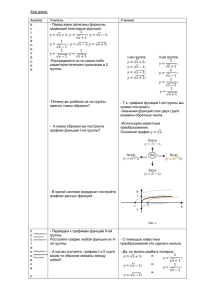
Тема урока «Как построить графики функций y=f(x+l), y=f(x)+m, y=f(x+l)+m, если известен

1
Тема урока
«Как построить графики функций y=f(x+l), y=f(x)+m, y=f(x+l)+m, если известен
график функции y=f(x)»
Цель: организовать деятельность учащихся по изучению и первичному закреплению знаний о
построении графиков функций y=f(x+l), y=f(x)+m, y=f(x+l)+m, если известен график функции
y=f(x)
Задачи:
 создание
условий
для
осознания,
осмысления учащимися
знаний
о
преобразованиях, которые позволят строить новые графики функций; для
формирования умений применять полученные алгоритмы к построению графиков
функции,
 формирование потребности в приобретении знаний, развитие кругозора,
любознательности, внимания.
 развитие культуры математической речи, привитие интереса к изучению
математики,
 изменение роли ученика в учебном процессе от пассивного наблюдателя до
активного исследователя.
Тип урока: урок изучения нового материала
Оборудование: компьютеры, проектор, экран, программа «Живая математика», презентация
«Как построить графики функций y=f(x+l), y=f(x)+m, y=f(x+l)+m, если известен график
функции y=f(x)», раздаточные материалы с заданиями практической работы и упражнениями.
Скажи мне - и я забуду,
Покажи мне - и я запомню,
Вовлеки меня в процесс - и я пойму,
Отойди - и я всё сделаю сам!
(Конфуций)
2
Ход урока
1. Организационный момент.
Цель - положительный настрой на организованную работу.
(Приветствие, проверка готовности уч-ся к уроку, организация внимания учащихся).
Сегодня мы продолжим изучение функций, их графиков и свойств.
2. Актуализация знаний.
(слайд 2 )
1. Перед вами три черных ящика.
Чтобы узнать, что в них скрыто, надо отгадать о какой функции идет речь по ее
свойствам.
1.
2.
3.
4.
5.
1.
2.
3.
4.
1.
2.
3.
4.
5.
6.
D(у)=(-  ;+  )
ограничена снизу
убывает при отрицательных значениях х., возрастает при положительных значениях х.
выпукла вниз
Наименьшее значение функции равно 0
(у=х2)
Не ограничена ни снизу, ни сверху
убывает на всей области определения
Ни наибольшего, ни наименьшего значений у функции нет
Функция имеет разрыв в точке х=0
(у=к/х)
возрастает
выпукла вверх
ограничена снизу, не ограничена сверху.
D(y) =[0; +  )
наименьшее значение функции равно 0.
Е(у)=[0; +  )
(y  x )
2. Определите значение коэффициента k для каждой параболы. (слайд 3 )
Задание выполняется самостоятельно, с последующей проверкой.
Проверка ответов (слайд 4 )
3
3. Этап подготовки учащихся к активному и сознательному усвоению нового
материала.
Необычный рисунок. Как вы думаете, какое отношение имеет этот лягушонок к нашему
разговору о графиках функций?
(он построен из участков парабол)
Вопрос учителя: Чем отличаются друг от друга эти параболы?
(направлением ветвей и координатами вершин)
Возникает вопрос, как задать эти параболы?
На уроке мы рассмотрим преобразования функций, в результате которых из известных нам
функций и их графиков появляются новые их виды. Наша цель – научиться строить графики
и задавать уравнения этих функций.
4. Изучение нового материала
Изучение нового материала построено в виде самостоятельной практической работы,
которую выполняет каждый ученик за компьютером.
4
Практическая работа
Используя программу «Живая математика», постройте в одной системе координат
графики каждой группы функций, сравните расположение графиков, сделайте вывод
(заполните пропуски в таблице)
График может быть получен из
графика функции
с
помощью сдвига ………. вдоль
оси … на … единиц
График может быть получен из
графика функции … с помощью
сдвига ……….вдоль оси…
на……. единиц
II
График может быть получен из
графика функции
с
помощью сдвига …… вдоль оси
…. на……. единиц
График может быть получен из
графика функции ... с помощью
сдвига …… вдоль оси …. На
… единиц
Вывод: Чтобы построить график функции
, где
, нужно
__________________________________________________________________________
__________________________________________________________________________
Чтобы построить график функции
, где
, нужно _________________
__________________________________________________________________________
III
График может быть получен из
графика функции
с помощью сдвига
………. на……. единиц
График может быть получен из
графика функции
….. с помощью сдвига ……….
на……. единиц
I
График может быть получен из
V
графика функции ….. с
помощью сдвига ………. на…….
единиц
График может быть получен из
графика функции ….. с
помощью сдвига ………. на…….
единиц
Вывод: Чтобы построить график функции
, где
, нужно
________________________________________________________________________
Чтобы построить график функции
, где
, нужно ______________
________________________________________________________________________
I
5
2. Подведение итогов практической работы.(построено в форме беседы с
сопровождением презентации) (слайды 6-9)
Как построить графики функций
,
Чтобы построить график функции
?
, где
, нужно сдвинуть график функции
y=f(x) вдоль оси х на l единиц влево.
Чтобы построить график функции
, где
функции y=f(х) вдоль оси х на l единиц вправо.
Как построить графики функций
, нужно сдвинуть график
,
?
Чтобы построить график функции
, где
функции y=f(x) вдоль оси Оу вверх на m единиц
, надо сдвинуть график
Чтобы построить график функции
, где
функции y=f(x) вдоль оси Оу вниз на m единиц.
, надо сдвинуть график
Как построить графики функций y=f(x+l)+m?
(ответы детей)
Комментирование построения графика на слайде. (слайд 10)
Алгоритм 2 построения графиков
1.Перейти к вспомогательной системе координат, проведя пунктиром прямые х = - l, у =
m.
2. К новой системе координат привязать график функции y=f(x).
Комментирование построения графика на слайде (слайд 11)
5. Закрепление.
1. Постройте графики функций
а) y  ( x  5) 2
в) y 
x 2
б) y  ( x  3) 2
г) y 
x 4
д) y  x  1  3
2. График какой функции получится, если:
Описание графика
1.
Параболу y  3x 2 перенести на 4 единицы влево вдоль оси Ох
2.
Гиперболу y 
7
перенести на 3 единицы вправо вдоль оси Ох
x
Уравнение
6
3.
График функции y 
4.
Параболу y  2x 2 перенести на 3 единицы вверх вдоль оси Оу
5.
График функции y  x перенести на 3 единицы вправо и на 1 единицу
x перенести на 2 единицы вниз вдоль оси Оу
вниз
3. (слайд 13)
Составьте уравнения парабол, из которых построен этот рисунок. Учитывайте области
определения функций, которые заданы этими уравнениями.
6. Домашнее задание.
Учебник, стр.117, алгоритмы 1,2 , выучить наизусть,
№ 20.7(а)-20.10(а), №20.14. № 19.3
7. Обобщение знаний, их систематизация. Рефлексия.
Цель - умение сделать математические выводы и объяснить их суть.
Какой общий вывод можно сделать для работы с графиками y = f(x+l), y = f(x)+m, если
известен график функции y = f(x)?