Простейшие преобразования графиков.
реклама
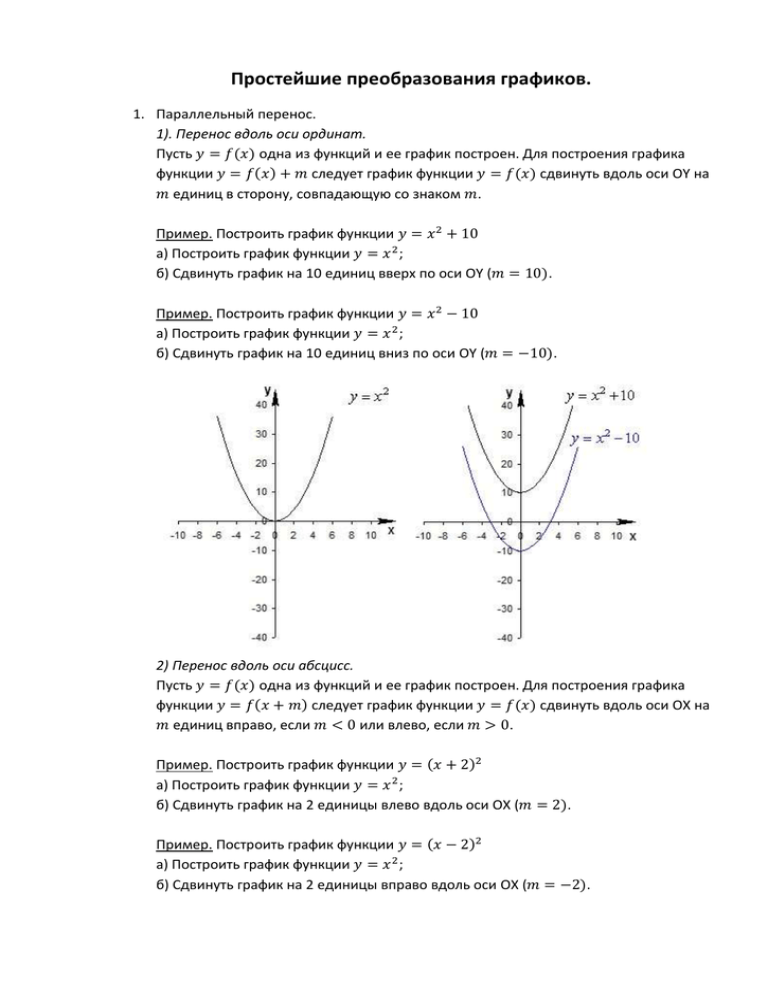
Простейшие преобразования графиков. 1. Параллельный перенос. 1). Перенос вдоль оси ординат. Пусть 𝑦 = 𝑓(𝑥) одна из функций и ее график построен. Для построения графика функции 𝑦 = 𝑓(𝑥) + 𝑚 следует график функции 𝑦 = 𝑓(𝑥) сдвинуть вдоль оси ОY на 𝑚 единиц в сторону, совпадающую со знаком 𝑚. Пример. Построить график функции 𝑦 = 𝑥 2 + 10 а) Построить график функции 𝑦 = 𝑥 2 ; б) Сдвинуть график на 10 единиц вверх по оси OY (𝑚 = 10). Пример. Построить график функции 𝑦 = 𝑥 2 − 10 а) Построить график функции 𝑦 = 𝑥 2 ; б) Сдвинуть график на 10 единиц вниз по оси OY (𝑚 = −10). 2) Перенос вдоль оси абсцисс. Пусть 𝑦 = 𝑓(𝑥) одна из функций и ее график построен. Для построения графика функции 𝑦 = 𝑓(𝑥 + 𝑚) следует график функции 𝑦 = 𝑓(𝑥) сдвинуть вдоль оси ОX на 𝑚 единиц вправо, если 𝑚 < 0 или влево, если 𝑚 > 0. Пример. Построить график функции 𝑦 = (𝑥 + 2)2 а) Построить график функции 𝑦 = 𝑥 2 ; б) Сдвинуть график на 2 единицы влево вдоль оси OX (𝑚 = 2). Пример. Построить график функции 𝑦 = (𝑥 − 2)2 а) Построить график функции 𝑦 = 𝑥 2 ; б) Сдвинуть график на 2 единицы вправо вдоль оси OX (𝑚 = −2). 2. Отражение. 1) Построение графика функции 𝑦 = 𝑓(−𝑥). Для построения графика функции 𝑦 = 𝑓(−𝑥) следует построить график функции 𝑦 = 𝑓(𝑥) и отобразить его относительно оси ординат. Пример. Построить график функции 𝑦 = √−𝑥 а) Построить график функции 𝑦 = √𝑥; б) Отобразить график функции относительно оси OY. 2) Построение графика 𝑦 = −𝑓(𝑥). Для построения графика функции 𝑦 = −𝑓(𝑥) следует построить график функции 𝑦 = 𝑓(𝑥) и отобразить его относительно оси абсцисс. Пример. Построить график функции 𝑦 = −𝑥 2 а) Построить график функции𝑦 = 𝑥 2 б) Отобразить график функции относительно оси абсцисс. 3. Деформация. 1) Сжатие графика вдоль оси ординат к оси ОХ 𝑦 = а𝑓(𝑥); 0 < а < 1. Для построения графика функции 𝑦 = а𝑓(𝑥) следует построить график функции 1 𝑦 = 𝑓(𝑥) и уменьшить его ординаты в а раз при 0 < а < 1. 2) Растяжение графика вдоль оси ординат от оси ОХ 𝑦 = а𝑓(𝑥); а > 1. Для построения графика функции 𝑦 = а𝑓(𝑥) следует построить график функции 𝑦 = 𝑓(𝑥) и увеличить его ординаты в а раз при а > 1. 1 Пример. Построить график функции 𝑦 = 𝑥 2 3 2 а) Построить график функции𝑦 = 𝑥 б) Уменьшить его ординаты в 3 раза. Пример. Построить график функции 𝑦 = 3𝑥 2 а) Построить график функции𝑦 = 𝑥 2 б) Увеличить его ординаты в 3 раза. 3) Растяжение графика вдоль оси абсцисс 𝑦 = 𝑓(𝑤𝑥); 0 < 𝑤 < 1. Для построения графика функции 𝑦 = 𝑓(𝑤𝑥)следует построить график функции 1 𝑦 = 𝑓(𝑥) и увеличить его абсциссы в 𝑤 раз при 0 < 𝑤 < 1. 4) Сжатие графика вдоль оси абсцисс 𝑦 = 𝑓(𝑤𝑥); 𝑤 > 1. Для построения графика функции 𝑦 = 𝑓(𝑤𝑥)следует построить график функции 𝑦 = 𝑓(𝑥) и уменьшить его абсциссы в 𝑤 раз при 𝑤 > 1. 1 Пример. Построить график функции 𝑦 = (3 𝑥) 2 а) Построить график функции𝑦 = 𝑥 2 б) Увеличить его абсциссы в 3 раза. Пример. Построить график функции 𝑦 = (3𝑥)2 а) Построить график функции𝑦 = 𝑥 2 б) Уменьшить его абсциссы в 3 раза. 4. Функции, содержащие знак модуля. 1) Построение графика функции 𝑦 = |𝑓(𝑥)|. Для построения графика функции 𝑦 = |𝑓(𝑥)| следует построить график функции 𝑦 = 𝑓(𝑥) и ту часть графика, которая расположена ниже оси OX, стереть, предварительно отобразив ее относительно оси абсцисс. Пример. Построить график функции 𝑦 = |𝑥 + 4| а) Построить график функции 𝑦 = 𝑥 + 4 б) Ту часть графика, которая лежит ниже оси OX, отобразить симметрично в верхнюю полуплоскость относительно оси OX. 2) Построение графика функции 𝑦 = 𝑓(|𝑥|). Для построения графика функции 𝑦 = 𝑓(|𝑥|). следует построить график функции 𝑦 = 𝑓(𝑥) при 𝑥 ≥ 0 и отобразить его относительно оси OY. Пример. Построить график функции 𝑦 = |𝑥| + 4 а) Построить график функции 𝑦 = 𝑥 + 4 б) Ту часть графика, которая лежит левее оси OY стереть, а ту часть, которая правее оси OY, отобразить симметрично в левую полуплоскость относительно оси OY. Примеры: