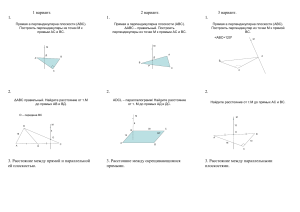
Перпендикуляр и наклонные.
реклама

41. Перпендикуляр и наклонные. Для решения задач необходимо напомнить свойства проекций, наклонной и перпендикуляра, теорему о трех перпендикулярах, формулу (лучше с выводом) нахождения медианы по сторонам треугольника, как устанавливается угол между прямой и плоскостью. Задачи [16,с.60-62], [37,с.24]. Литература Задача 1. Плоскость проходит через основание трапеции на расстоянии 8см от средней линии и на расстоянии 10см от точки пересечения диагоналей трапеции. Найдите отношение длин оснований трапеции. Решение. C Q B плоскости (рис.1), тогда sin O O M Пусть - угол наклона плоскости трапеции к C N O1 P K D A sin A Рис.1 P K D Рис.2 82 CK OP 10 5 . CK 16 8 OO1 10 OP OP На рис.2 вынесен АСD. Имеем: АОР АСК ( А общий, ОР||СК по трем углам) АО ОР 5 АС СК 8 С другой стороны ВОСAOC по трём углам (ВОС=АОD- как вертикальные, другие накрест лежащие). ВС OC АD AO , т.к. AC AO OC OC 8 OC 3 BC 3 1 . AO AO AO 5 AO 5 AD 5 Задача 2. Точка М удалена от вершины угла ВАС, равного 60, на 25см, а от сторон АВ и АС на 20см и 7см. Найдите расстояние от точки М до плоскости АВС. Решение: Задача 3. Точки А и С находятся в плоскости , а точки В и D в плоскости , причем АВ=9см, CD=15cм, АС=7см, ВD=11cм и отрезок АВ перпендикулярен плоскостям и . Найдите расстояние между серединами отрезков АВ и СD. Решение. Пусть М и К соответственно середины АВ и СD. Спроектируем на АВ и СD. C A M K B D O E В проекция точек А и М (АВ). пусть Е и Осоответственно проекции точек С и К АВ||KO||CE точки М, В, К, О лежат в одной плоскости, также и В, А, С, Е. МВКО, ВАСЕ прямоугольники (четырехугольники, полученные пересечением пар параллельных прямых). МК=ВО, АС=ВЕ, СЕ=АВ. BD 2 BE 2 DE 2 ВОмедиана ВЕD ВО 2 . 2 4 ВD=11, BE=7, DE CD 2 CE 2 152 9 2 12 (см). Отсюда ВО , 121 49 144 7(см). Искомое расстояние МК=7см. 2 4 Задача 4. Плоскость параллельна гипотенузе АВС. Проекции сторон треугольника на плоскость соответственно равны 51см, 43см, 20см. Определите периметр и площадь АВС. Решение: Задача 5. Стороны АВС равны 15см, 15см, 24см. Точка М удалена от каждой из прямых АВ, АС, ВС на 12см. Найдите расстояние от точки М до плоскости АВС. Решение: Задача 6. Из точки М опущены перпендикуляры: МО на плоскость АВС, МD и МЕ на стороны АВ и АС равностороннего треугольника, периметр которого Р=72см. Известно, что точка ОВС, а углы между МD и МЕ и плоскостью треугольника составляют 30и 60.Найдите длину МО. Решение: Содержание