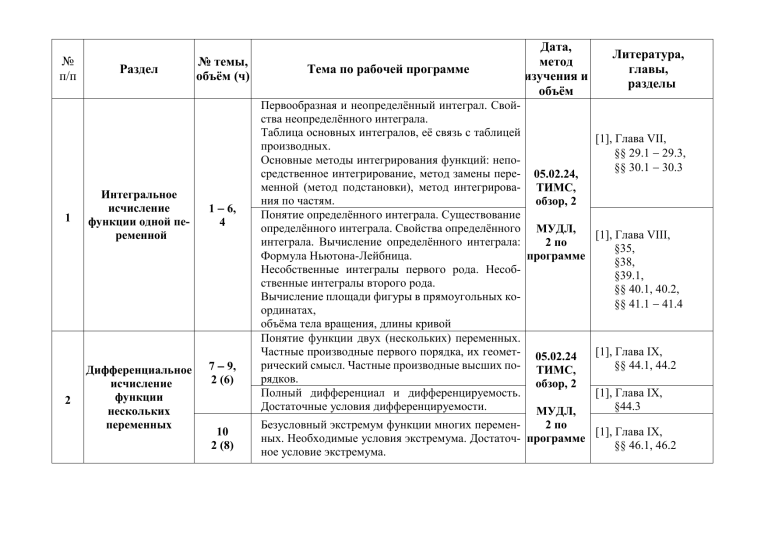
№ п/п Раздел 1 Интегральное исчисление функции одной переменной 2 Дифференциальное исчисление функции нескольких переменных № темы, объём (ч) 1 6, 4 7 9, 2 (6) 10 2 (8) Тема по рабочей программе Дата, метод изучения и объём Литература, главы, разделы Первообразная и неопределённый интеграл. Свойства неопределённого интеграла. Таблица основных интегралов, её связь с таблицей [1], Глава VII, производных. §§ 29.1 29.3, Основные методы интегрирования функций: неп 30.1 30.3 средственное интегрирование, метод замены пере- 05.02.24, менной (метод подстановки), метод интегрирова- ТИМС, ния по частям. обзор, 2 Понятие определённого интеграла. Существование определённого интеграла. Свойства определённого МУДЛ, [1], Глава VIII, интеграла. Вычисление определённого интеграла: 2 по §35, Формула Ньютона-Лейбница. программе §38, Несобственные интегралы первого рода. Несоб§39.1, ственные интегралы второго рода. §§ 40.1, 40.2, Вычисление площади фигуры в прямоугольных к 41.1 41.4 ординатах, объёма тела вращения, длины кривой Понятие функции двух (нескольких) переменных. Частные производные первого порядка, их геомет- 05.02.24 [1], Глава IX, рический смысл. Частные производные высших по- ТИМС, §§ 44.1, 44.2 рядков. обзор, 2 Полный дифференциал и дифференцируемость. [1], Глава IX, Достаточные условия дифференцируемости. §44.3 МУДЛ, 2 по Безусловный экстремум функции многих перемен[1], Глава IX, ных. Необходимые условия экстремума. Достаточ- программе §§ 46.1, 46.2 ное условие экстремума. 3 4 Кратные интегралы 11, 12, 2 (10) Двойной интеграл и его свойства. Вычисление двойного интеграла. Некоторые приложения двойного интеграла: вычисление площади поверхности, объёма тела, 13, 2 (12) Понятие о тройном интеграле, его вычислении и некоторых геометрических приложениях 14 17, 2 (14) Задача, приводящая к дифференциальному уравнению. Понятие дифференциального уравнения (ДУ), его решения. Общий интеграл ДУ. Задача Коши, существование и единственность её решения. Уравнения первого порядка. Уравнения с разделяющимися переменными. Однородные уравнения первого порядка и уравнения, приводящиеся к ним. Линейные уравнения первого порядка. Методы Бернулли (Коши) и вариации постоянной. 18 20, 2 (16) Уравнения, допускающие понижение порядка. Линейные уравнения высших порядков. Теоремы о линейной комбинации решений однородного уравнения. Фундаментальная система решений. Метод вариации произвольных постоянных. Линейные уравнения с постоянными коэффициентами. Структура решений. Дифференциальные уравнения Литература. 1. Д.Т. Письменный. Конспект лекций по высшей математике. 9-е изд. М.: Айрис. 2009. 2. К.Н. Лунгу. Сборник задач по высшей математике, 1 курс.








