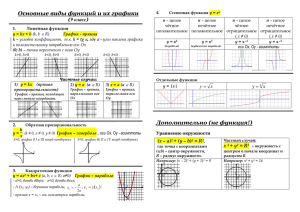
Теория
В задании 11 материалов ОГЭ проверяются
навыки работы с видами функций:
Линейная
у=кх+b
Обратно
пропорциональная
к
у=
Квадратичная
у=ах2 +bх+с
х
График - прямая
График - парабола
График - гипербола
Функция квадратного корня
Ветвь параболы,
симметричной относительно
оси y=a 𝑥, a≠ 0
Линейная функция
• Задается уравнением вида у=кх+b. Графиком
функции является прямая. Коэффициенты к и b
определяют расположение прямой на координатной
плоскости.
Коэффициент к:
• Определяет в какой координатной
плоскости располагается прямая:
к>0
к<0
Прямая находится в первой и Прямая находится во второй и
третьей координатной
четвертой координатной
четверти
четверти
I
Ш
II
IV
Коэффициент B:
• Определяет смещение прямой вверх или вниз
вдоль оси ординат (Оу)
b>0
Прямая смещается вверх
вдоль оси Оу на b единиц
b
{
b<0
Прямая смещается вниз вдоль
оси Оу на b единиц
}
b
Определите знак коэффициентов b и к у
данной прямой
I
b
III
{
Прямая
проходит
через
I
и
III
координатные
четверти,
значит
коэффициент к>0
Прямая смещена вниз
на четыре единицы
вдоль оси ординат,
значит b<0
Определите знак коэффициентов b и к у данной
прямой
Прямая проходит через
II и IV координатные
четверти,
значит
коэффициент к<0
II
b
{
IV
Прямая
смещена
вверх
на
четыре
единицы вдоль оси
ординат, значит b>0
Квадратичная функция
• Задается уравнением вида у=ах2 +bх+с
Графиком функции является парабола. Коэффициенты
а, b и с определяют расположение прямой на
координатной плоскости.
Вершина параболы:
𝒃
𝒙𝟎 = −
𝟐𝒂
𝒚𝟎 = 𝒇(𝒙𝟎 )
09:16
10
Коэффициент А:
Определяет направление ветвей параболы:
а>0
а<0
Ветви параболы направлены Ветви параболы направлены
вниз
вверх
Коэффициент В:
• Определяет смещение параболы вправо
или влево вдоль оси абсцисс (Ох)
b<0
{
Парабола смещена вправо
вдоль оси абсцисс
{
b>0
Парабола смещена влево
вдоль оси абсцисс
b>0
b<0
Коэффициент с:
• Определят положение точки пересечения
параболы с осью ординат (Оу)
с>0
с<0
Парабола пересекает ось Оу в Парабола пересекает ось Оу в
положительном направлении отрицательном направлении
с>0
с<0
Определите знаки коэффициентов а, b и с
данной параболы
Ветви
параболы
направлены
вверх,
значит
коэффициент
а>0
Парабола смещена
вправо вдоль оси
абсцисс, значит
коэффициент b<0
Парабола пересекает
ось
ординат
в
отрицательном
направлении, значит
коэффициент с<0
Обратно-пропорциональная
функция
к
• Задается уравнением вида у=х
Графиком функции является гипербола.
Коэффициент, к определяет расположение
прямой на координатной плоскости.
Чем больше модуль К,
тем график дальше от осей
Коэффициент к:
• Определяет расположение ветвей
гиперболы в координатных четвертях
к<0
к>0
Ветви гиперболы находятся в Ветви гиперболы находятся во
первой и третьей
второй и четвертой
координатной четверти
координатной четверти
I
III
II
IV