grafiki_funkcii

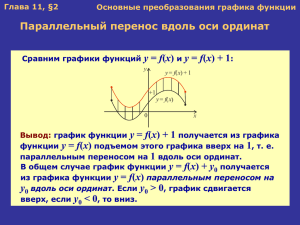
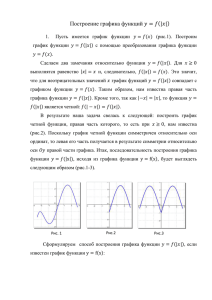
Графики функций
2
2
y = ax + n и a(x – m)
Цели:
•
•
•
рассмотреть параллельный перенос графика функции.
развивать мыслительные способности учащихся, умение
анализировать, выделять общие и отличительные свойства;
развитие исследовательских способностей; умений применять
теоретические знания на практике; развитие памяти, внимания,
наблюдательности;
воспитывать устойчивый интерес к изучению математики,
стимулировать учащихся к самовыражению, создавая
ситуацию успеха для каждого
I. Сообщение темы и цели урока
II. Повторение и закрепление
пройденного материала
1. Ответы на вопросы по домашнему
заданию (разбор нерешённых задач).
2. Контроль усвоения материала
(письменный опрос).
Вариант 1
1. Приведите основные
свойства и график
2
функции y  ax при a  0.
2. Постройте график функции
3
2
2
x

x
а) y  2 x ; б) y 
x 1
3. При каком значении а
прямая у = х + а касается
параболы y  0,5x 2?
Вариант 2
1. Приведите основные
свойства и график
2
функции y  ax при a  0.
2. Постройте график функции.
2
3
1
2
x

x
y  x ; б) y 
3
x 1
3. При каком значении а
прямая у = х – а касается
параболы y  2x 2?
III. Изучение нового материала
Два важнейших преобразования
графика функции y  f  x 
1. График функции y  f  x 
получается из графика функции
y  f x 
с помощью симметрии
относительно оси абсцисс.
2. График функции y  af  x  из
y  f x 
растяжением вдоль оси ординат в
а раз при а > 1
1
и сжатием в раз при 0  a  1
a
Эти преобразования пригодны для любых функций (как
изученных, так и ещё не рассмотренных).
y  f x   n
y  f x  m
y  f x 
параллельного
параллельного
переноса вдоль
переноса вдоль
оси ординат на n оси абсцисс на m
единиц: вправо
единиц: вверх
при п > 0 и вниз при т > 0 и
влево при т < 0.
при п < 0.
Пример 1
Построим график функции
2
y  x  2
2
y  x
параллельным переносом вдоль
оси ординат на 2 единицы вниз
y
0
-1
-2
x
y  x
2
2
y  x  2
Пример 2
2
Построим график функции y   x  1
2
y   x    1 
2
yx
параллельным переносом вдоль оси
абсцисс на 1 единицу влево
y
y   x  1
yx
2
-1 0
2
x
y  f x  m  n
y  f x 
два параллельных переноса:
Эти сдвиги можно выполнять в
любом порядке: сначала вдоль оси
абсцисс, а затем вдоль оси ординат
или наоборот.
Пример 3
Построим график функции
2
1
y    x  2  1
2
1. Строим график функции y  x
2
2. y   x
1
2
3. y   x
2
1
2
4. y   x  1
2
2
1
5. y    x  2   1
2
2
y
yx
2
1
1
-1
2
x
2
1
y    x  2  1
2
IV. Контрольные вопросы
1. Алгоритм построения графика
функции y  f  x 
2. Как построить график функции
y  af  x  при a  0
3. Построение графика функции
y  f x   n
4. Алгоритм построения графика
функции y  f  x  m 
V. Задание на уроке
№ 106 (а, в); 107 (а); 109 (а, в, д);
110 (б, в); 114; 116 (а, в); 117 (а);
118 (а, б).
VI. Задание на дом
№ 106 (б, г); 107 (б); 109 (б, г, е);
110 (а, г); 115; 116 (б, г); 117 (б);
118 (в, г).
VII. Подведение итогов урока