4.графический способ решения уравнений Дивавин А.8Б

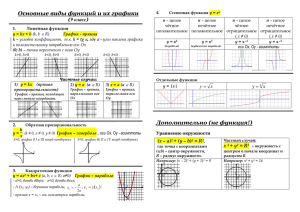
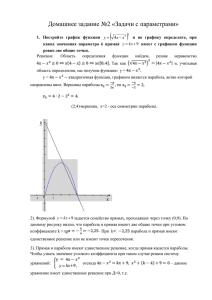
Выполнил : ученик 8 класса Б
МБОУ “Лицей No1”
города Тулы
Дивавин Артём
Учитель : Смирнова Екатерина Алексеевна
Графический способ решения уравнения состоит в
построении на одной координатной плоскости
графиков двух функций и нахождении абсцисс их
точек пересечения (если такие точки есть).
В случае квадратного уравнения строятся графики
квадратичной и линейной
функций – парабола и прямая.
Возможны следующие случаи:
 1)Прямая и парабола касаются
(имеют единственную общую точку),
абсцисса точки касания –
корень уравнения.
 2)Прямая
и парабола
пересекаются в двух
точках, абсциссы этих
точек являются корнями
уравнения(рис.1).
 3)Прямая
и парабола
не имеют общих точек,
тогда уравнение не имеет
корней(рис.2).
Решение. Перепишем уравнение в виде
х2=-1.5x+2.5.
Рассмотрим функции y= х2 и у=-1.5х+2.5.
Построим в одной координатной плоскости графики этих
функций и найдём абсциссы
их точек пересечения: x1=-2.5,
x2=1. Эти числа являются
корнями исходного уравнения.
Ответ:-2.5, 1.
 а)х2=0;
 б)2х2+7=0;
 в)х2-2х=0.
а) x2=0;
Построим в одной координатной плоскости
графики функций y=x2 и y=0.
y=0;
Функция – линейная.
График функции – прямая,
совпадающая с осью абсцисс.
y=x2
График функции – парабола.
Составим таблицу значений функции:
x
-3
-2
-1
-0.5
0
0.5
1
2
3
y
9
4
1
0.25
0
0.25
1
4
9
Ответ : х=0.
б) 2х2+7=0; х2=-3.5.
Построим в одной координатной плоскости графики
функций y=х2 и y=-3.5.
y=-3.5;
Функция – линейная.
График функции – прямая,
параллельная оси абсцисс
и пересекающая ось ординат
в точке с координатами
(0;-3.5).
y=х2
График функции – парабола.
Составим таблицу значений функции:
x
-3
-2
-1
-0.5
0
0.5
1
2
3
y
9
4
1
0.25
0
0.25
1
4
9
Ответ : нет корней.
в)х2-2х=0;х2=2х.
Построим в одной координатной плоскости графики
функций у=х2 и у=2х.
у=2х;
Функция – прямая
пропорциональность
График функции – прямая,
проходящая через начало
координат и точку с
координатами (2;4).
y=x2
График функции – парабола.
Составим таблицу значений функции:
x
-3
-2
-1
-0.5
0
0.5
1
2
3
y
9
4
1
0.25
0
0.25
1
4
9
Ответ : х=0 и х=2.