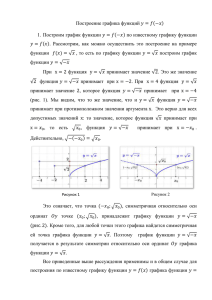
Тема «Построение графика функций y=f(|x|)».

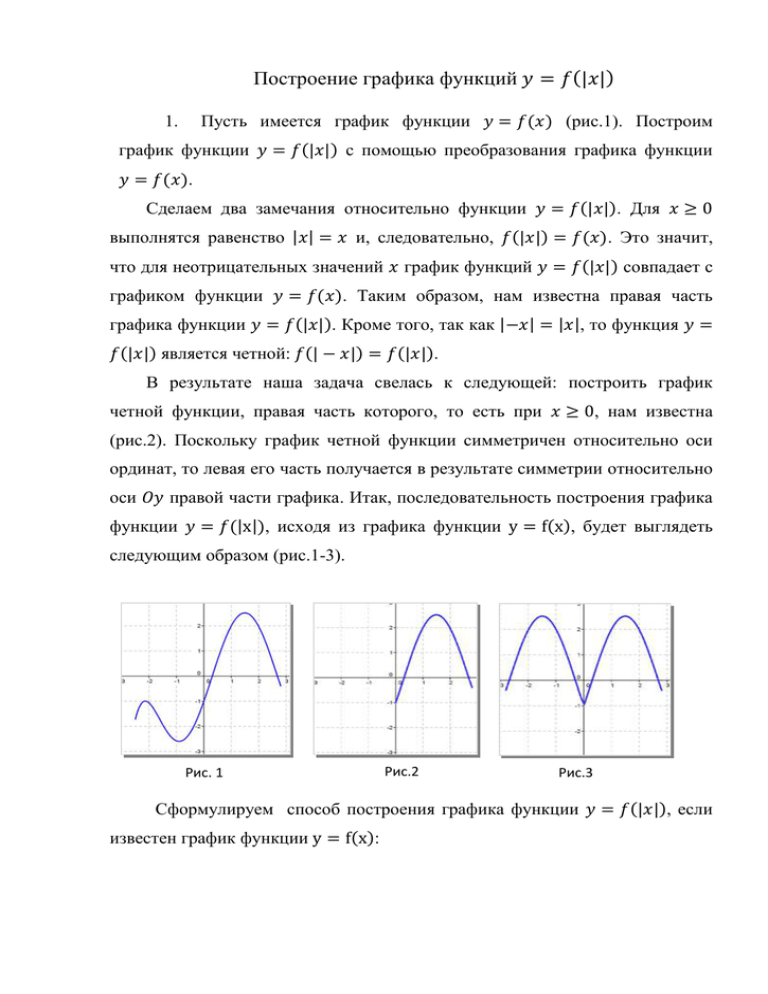
Построение графика функций 𝑦 = 𝑓 (|𝑥|)
Пусть имеется график функции 𝑦 = 𝑓(𝑥) (рис.1). Построим
1.
график функции 𝑦 = 𝑓(|𝑥|) с помощью преобразования графика функции
𝑦 = 𝑓(𝑥).
Сделаем два замечания относительно функции 𝑦 = 𝑓(|𝑥|). Для 𝑥 ≥ 0
выполнятся равенство |𝑥| = 𝑥 и, следовательно, 𝑓(|𝑥|) = 𝑓(𝑥). Это значит,
что для неотрицательных значений 𝑥 график функций 𝑦 = 𝑓(|𝑥|) совпадает с
графиком функции 𝑦 = 𝑓(𝑥). Таким образом, нам известна правая часть
графика функции 𝑦 = 𝑓(|𝑥|). Кроме того, так как |−𝑥| = |𝑥|, то функция 𝑦 =
𝑓(|𝑥|) является четной: 𝑓(| − 𝑥|) = 𝑓(|𝑥|).
В результате наша задача свелась к следующей: построить график
четной функции, правая часть которого, то есть при 𝑥 ≥ 0, нам известна
(рис.2). Поскольку график четной функции симметричен относительно оси
ординат, то левая его часть получается в результате симметрии относительно
оси 𝑂𝑦 правой части графика. Итак, последовательность построения графика
функции 𝑦 = 𝑓(|x|), исходя из графика функции y = f(x), будет выглядеть
следующим образом (рис.1-3).
Рис. 1
Рис.2
Рис.3
Сформулируем способ построения графика функции 𝑦 = 𝑓(|𝑥|), если
известен график функции y = f(x):
𝒇|𝒙|
𝒇(𝒙)
Чтобы получить график функции 𝒇|𝒙|
из графика функции 𝒇(𝒙) необходимо:
 оставить без изменений часть графика функции 𝒇(𝒙), лежащую
правее оси ординат Oy
 отразить
симметрично
относительно
оси
ординат
Oy
часть
графика функции 𝒇(𝒙), лежащую правее этой оси
Заметим, что если график функции 𝑦 = 𝑓(𝑥) целиком располагается
левее оси ординат или, другими словами, область определения функции 𝑦 =
𝑓(𝑥) состоит только из отрицательных чисел, то функцию 𝑦 = 𝑓(|𝑥|)
определить не удастся, поскольку |𝑥| ≥ 0.
2. Пример 1. Построить график функции y = x 2 − 2|x| − 2.
Формулу функции можно записать в виде y = |x|2 − 2|x| − 2. Поэтому,
если взять 𝑓(𝑥) = x 2 − 2x − 2, то 𝑓(|𝑥|) = |x|2 − 2|x| − 2. Таким образом,
сначала построим график функции y = x 2 − 2x − 2 (рис.4).
Рис. 4
Рис. 5
Затем преобразуем его по описанному выше правилу. Часть параболы,
которая лежит правее оси ординат Oy, оставим без изменений, а часть
параболы, лежащую левее оси 𝑂𝑦, «сотрем». Затем в левую полуплоскость
отразим симметрично относительно оси 𝑂𝑦 часть параболы, которая лежит
правее оси ординат Oy. В результате получаем график функции y = x 2 −
2|x| − 2 (рис.5).
Пример 2. Построить график функции y = 2|x| − 1|.
Построим график линейной функции y = 2𝑥 − 1, то есть прямую.
Далее, ее часть, лежащую справа от оси ординат, симметрично отображаем
относительно оси ординат. В результате получаем график функции y =
2|x| − 1|.
a)
b)
Рис. 6
Заметим, что этот график можно было построить и другим способом,
взяв
в
качестве
последовательно
исходного
график
растяжение и
сдвиг:
функции
y = |𝑥|
и
применяя
y = |𝑥| ⟹ y = 2|𝑥| ⟹ 𝑦 =
2|x| − 1| (рис.6). Однако, первый способ оказался рациональнее.
Исходя из способа построения графика функции 𝑦 = 𝑓(|𝑥|) можно
сделать вывод, что область определения функции 𝑦 = 𝑓(|𝑥|) симметрична
относительно нуля, причем для 𝑥 ≥ 0 она совпадает с 𝐷(𝑓). Множество
значений функции 𝑦 = 𝑓(|𝑥|) состоит из тех значений функции 𝑦 = 𝑓(𝑥),
которые получаются при неотрицательных значениях аргумента 𝑥 ∈ 𝐷(𝑓).
Упражнения
1. На рисунке изображен график функции y = f(x). Постройте график
функции y = f(|x|). Найдите область определения и множество
значений функции y = f(|x|).
2. Постройте график функции.
a) 𝑦 = 1 − |𝑥|
b) 𝑦 = 𝑥 2 + 2|𝑥||
c) 𝑦 = −𝑥 2 + 2|𝑥|
1
e) 𝑦 = |𝑥|+1
d) 𝑦 = 𝑥 2 − 5|𝑥| + 6
f) 𝑦 = |(|𝑥| − 1)3 |
3. Функция y = f(x) определена на всей числовой прямой. Для всякого
неотрицательного значения переменной х значение этой функции
совпадает со значением функции g(x) = x(x + 1)(5x − 2)(x + 5).
Сколько корней имеет уравнение f(|x|) = 0? Ответ: 3
4. Найдите область определения функции 𝑦 = 𝑓(|𝑥|), если известна
область определения функции 𝑦 = 𝑓(𝑥)
a)
c)
e)
g)
[−7; 2]
[−2; −1) ∪ (−1; 2]
[−1; 0) ∪ (0; 1)
(−∞ ; +∞)
b)
d)
f)
h)
[−5; 5)
[−1; 0) ∪ (0; 3]
(−∞ ; 1)
[3; 4]
5. На рисунке изображен график функции y = f(x). Решите уравнение
𝑓(|𝑥|) = 0. Сколько отрицательных корней имеет уравнение 𝑓(|𝑥|) =
1, 𝑓(|𝑥|) = −0,5, 𝑓(|𝑥|) = 2.
6. Приведите пример функции, для которой выполняется равенство
𝑓(|𝑥|) = |𝑓(𝑥)| при всех 𝑥 ∈ 𝐷(𝑓)?
7. Нарисуйте график такой функции 𝑦 = 𝑓(𝑥), что уравнение 𝑓(𝑥) = 0
имеет два корня, а уравнение 𝑓(|𝑥|) = 0 корней не имеет.