1 - slepenkova.ru

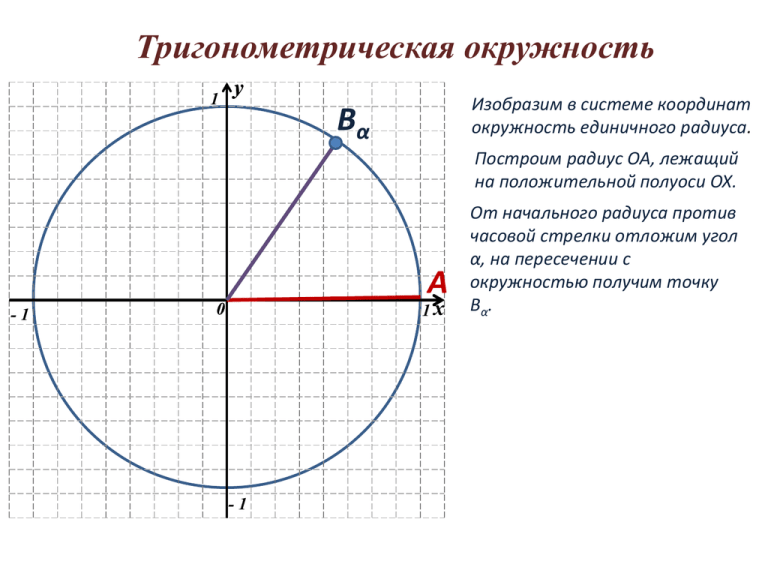
Тригонометрическая окружность
1
y
Изобразим в системе координат
окружность единичного радиуса.
Вα
Построим радиус ОА, лежащий
на положительной полуоси ОХ.
А
-1
1x
0
-1
От начального радиуса против
часовой стрелки отложим угол
α, на пересечении с
окружностью получим точку
Вα.
Тригонометрическая окружность
y С
1
90° (H450° )
D180°
-1
0
F270° - 1(J630° )
G360° (M1080° )
1
Тригонометрическая окружность
y С
1
-270° (H-630° )
D-180°
-1
0
F-90° - 1(J-450° )
G-360° (M-1080° )
1
Какой четверти принадлежит точка?
II Р125°
Р-240°
1
y
а) Р30° ϵ I четверти
б) Р240° ϵ IIIчетверти
Р30°
в) Р-240° ϵ II четверти
Р-340°
г) Р125° ϵ II четверти
0
-1
I
1
Р1040°
III
Р240°
-1
Р1040° IV
д) Р-340° ϵ I четверти
е) Р1040° ϵ IVчетверти
ж) Р-800° ϵ IVчетверти
1.1.4 На окружности
отметьте точки,
соответствующие углам:
а) -5400;
б) 8100;
в) -11700;
г) 13500;
д) -12600;
е) 15300
-540°
В
(В-1260°)- 1
В810°
1
y
В-1530°
0
В-1170° - 1(В1350°)
1
1.1.5 В какой четверти
будет лежать точка:
а) Р30° ϵ I четв.;
б) Р-230° ϵ III четв.;
в) Р-560° ϵ III четв.;
г) Р130° ϵ II четв.;
д) Р-228° ϵ II четв.;
ж) Р1254° ϵ II четв.;
з) Р-1347° ϵ III четв.;
и) Р-730° ϵ IV четв.;
к) Р-50° ϵ IV четв.;
Изображение на тригонометрической окружности
некоторых углов
1
y
F
E
С
1
2
-1

1
2
Рассмотрим прямоугольные
треугольники OCD и OFE.
0
1
2

Возьмем
тригонометрическую окружность
и
проведем
через
середины
единичных
отрезков
прямые,
параллельные соответствующим
осям.
1
2
-1
D 1x
∆ OCD = ∆ OFE ( по катету и
гипотенузе)
Следовательно дуги АС, СF и
FM равны между собой и равны
300.
Вся окружность оказалась
поделена на двенадцать равных
между собой дуг, с градусной мерой
300.
Изображение на тригонометрической окружности
углов, градусная мера которых кратна 300.
Р120°
1
y
Р780°
Р-210°
Р30°
1
2
Р360°
-1

1
2
0

Р210°
Р-120°
1x
1
2
1
2
-1
Р330°
Р-60°
№ 1.1.6
а) 300
б) 1200
в) 2100
г) 3300
д) 7800
е) - 600
ж) – 1200
з) - 2100
и) - 3600
Изображение на тригонометрической окружности
углов, градусная мера которых кратна 450.
1
y
Р135°
Р45°
1
2
-1

1
2
0
1
2

1x
1
2
Р315°
Р225°
-1
Р270°
№ 1.1.7
а) 45 0
б) 1350
в) 2250
г) 3150
д) 2700
№ 1.1.8
1
y
Р45°
Р150°
1
2
-1

1
2
0
1x
1
2

1
2
Р-390°
Р-135°
Р-90° - 1
Р-60°
а) 1500
б) 450
в) - 600
г) - 900
д) -1350
е) - 3900
№ 1.1.9
Р90° 1
Р480°
y
Р60°
Р-315°
1
2
-1

1
2
0
1
2

Р-150°
1x
1
2
Р-405°
-1
а) 900
б) 600
в) - 3150
г) 4800
д) -1500
е) – 4050
№ 1.1.10
1
y
Р-300°
Р495°
Р-330°
1
2
-1

1
2
0

Р570°
Р595°
1x
1
2
1
2
-1
Р-780°
а) 4950
б) -3300
в) 5700
г) - 3000
д) 5950
е) – 7800
Р1560°
№ 1.1.11
Р-1170° y
Р-1020°
Р765°
Р1110°
1
1
2
-1

1
2
0
1
2

Р1320°
1
2
-1
1x
а) 11100
б) -10200
в) 7650
г) 15600
д) 13200
е) – 11700
Определения синуса, косинуса, тангенса и котангенса
произвольного угла
1
y
Вα(x?α;y?α )
yyαα
sin α =
cos α =
-1
0
xxα
α
-1
1x
1
y
Вα
yα
Вβ
Определения синуса,
косинуса, тангенса и
котангенса
произвольного угла
sinβ
sinα
yβ
cosβ
α
cosα
0
ось синусов
xβ
- 1ось косинусов
β
-1
xα
1x
1
cosγ
sinγ
sinφ
0
yφ
Вγ
y
φγ
xγ
-1
Определения синуса,
косинуса, тангенса и
котангенса
произвольного угла
yγ
-1
xφ
cosβ
1x
Вφ
Значения синуса, косинуса, тангенса и котангенса
некоторых углов
1
y
Рассмотрим
прямоугольный ∆OCD:
CD= ½;
С(
1
2

1
2
0
1
2

1
2
-1
Тогда по теореме
Пифагора:
OD=
1
D
-1
; )
1
2
1x
ОС=1
.
Значения синуса, косинуса, тангенса и котангенса
некоторых углов
1
y
F(
E
; )
С(
1
2

1
2
0
1
2

; )
∆ OEF = ∆ OCD
(по гипотенузе и катету)
1
D
-1
Рассмотрим ∆ OEF :
1
2
1x
1
2
-1
Таким образом легко находятся
значения синуса, косинуса,
тангенса и котангенса углов
кратных 300.
№ 1.1.12
В-2700
В1200
1
y
-300
1200
1500
-2700
2100
-3300
sin α
В-3300
В1500
cos α
tg α
ctg α
-1
0
1
В2100
В-300
-1
sin α
1
cos α
0
tg α
не
существ.
ctg α
0
Значения синуса, косинуса, тангенса и котангенса
некоторых углов
1
y
S(
Рассмотрим треугольник OSH,
прямоугольный и равнобедренный:
)
OS = 1
По теореме Пифагора:
SH2 + OH2 = SO2.
;
1
Тогда SH = OH =
H
-1
0
Следовательно, известны
1
-1
.
координаты точки S.
№ 1.1.13
1
y
В1350
-450
В450
В-1800
0
-1
В-450
В2700
-1
-1800
sin α
0
cos α
˗1
tg α
˗1
˗1
0
ctg α
˗1
˗1
не
существ.
-1350
2700
450
1
В-1350
1350
sin α
˗1
cos α
0
tg α
1
ctg α
1
не
существ.
0
1
1
№ 1.1.14
1
y
В-3000
В-3150
В1500
0
-1
В2250
В2400
1
-1
В3000
№ 1.1.15
В-6000
1
y
В-7500
0
-1
1
-1
В11100
В31500
-1
В1140
0
-18600
№ 1.1.16
1
-1
y
0
1
-1
№ 1.1.17
1
-1
y
0
1
-1