Тригонометрические функции любого угла

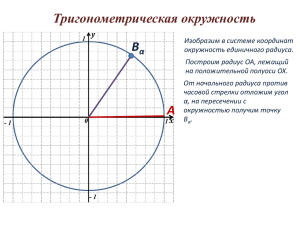
Тригонометрические
функции любого угла
Определение синуса, косинуса,
тангенса и котангенса.
Цели урока: изучить понятия синуса, косинуса, тангенса
и котангенса произвольного угла; рассмотреть
свойство сохранения значения при изменении угла
на целое число оборотов
Задачи: Ввести понятие синуса, косинуса,
тангенса и котангенса произвольного угла;
закрепить
ЗУН
нахождения
значений
выражений, содержащих синусы косинусы,
тангенсы и котангенсы углов 0,30, 45,
60,
90
градусов.
Учить
правильно
использовать терминологию; Прививать
интерес к предмету через применение
компьютера;
Внимание!
ОА – начальный радиус, a – угол поворота,
a =50˚
Поворот начального радиуса ОА около точки О
против часовой
, в радиус ОВ, а >0, а по
часовой
в радиус ОС, а <0,
Существует бесконечно много углов поворота,
при которых начальный радиус ОА перехоит в один и тот же радиус.
По часовой стрелке – угол положительный,
у
против
часовой стрелки В
угол
отрицательный.
а
А
О -а
С
х
Существует формула
Соответствующие углы поворота будут равны:
a + 360˚∙n,
где n-любое целое число
Если ∟АОВ=130˚, то соответствующие углы
поворота будут равны 130˚+360˚∙n.
При прибавлении к углу целого числа оборотов
получается угол той же четверти.
Например угол в 430˚ является углом I
четверти, так как 430˚= 360˚+ 70˚, а 70˚ в I
четверти
например
• 450, 4050, 7650, -3150 и т. д.
•
•
•
•
•
а =450+3600·n, n = целое число.
Если n=0, то а = 450
Если n=1, то а = 450+3600·1=4500
Если n=2, то а = 450+3600·2 =7650
Если n=-1, то а = 450+3600·(-1)=-3150.
Какой четверти угол?
•
•
•
•
Если 00 <a <900 , то угол а – угол I четверти
Если 900 <a <1800 , то угол а – угол II четверти
Если 1800 <a <2700 , то угол а – угол III четверти
Если 2700 <a <3600 , то угол а – угол IV четверти
90
II
I
0
180
III
IV
270
360
Определения
• Синусом угла а называется отношение
ординаты точки В к длине радиуса:
sina=y:R.
• Косинусом угла а называется отношение
абсциссы точки В к длине радиуса:
• cosa =x:R.
• Тангенсом угла а называется отношение
ординаты точки В к её абсциссе : tga=y:x.
• Котангенсом угла а называется отношение
абсциссы точки В к её ординате: ctga=y:х.
Определение градусной меры угла
по единичной окружности
Нахождение синуса, косинуса,
тангенса и котангенса