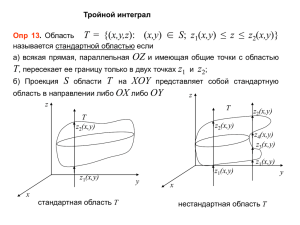
Применение интеграла в физике и технике
реклама
Применение интеграла в физике и технике Токунова Мария, Токунова Маргарита, Бадаева Тамара, Гусева Анастасия. Объем цилиндрического тела. Двойной интеграл. Цилиндрическим телом называется тело, ограниченное плоскостью Оxy, поверхностью, с которой любая прямая, параллельная оси Оz, пересекается не более чем в одной точке, и цилиндрической поверхностью, образующая которой параллельна оси Оz. Z X 1) Если разбить тело на части, то его объем будет равен сумме объемов всех частей; 2) Объем прямого цилиндра, т.е. цилиндрического тела, ограниченного плоскостью Оху, равен Y площади основания, умноженной на высоту тела. Объем n-ступенчатого тела равен: n Vn f ( x1 , y1 ) 1 f ( x2 , y2 ) 2 ... f ( xn , yn ) n f ( xi , yi ) i i 1 При n→∞ n V lim Vn lim f ( xi , yi ) i i 1 Объем цилиндрического тела с основанием D. f ( x , y ) d ( x , y ) dxdy . z D Z=f (x; y) D b V S ( x)dx a V D у a E b C х y2 ( x ) f ( x, y )dxdy f ( x, y )dy dx a y1 ( x ) b f ( x, y)dxdy dx D D b a y2 ( x ) f ( x, y)dy y1 ( x ) d f ( x, y)dxdy dy c x2 ( y ) f ( x, y)dx x1 ( y ) Вычислим двойной интеграл x y D ( x y)dxdy 0 dx 2 ( x y)dy 0 xy 2 2 dx x x 1 x 1 2 4 3 4 5 2 x2 1 x x x x 3 3 0 x 2 x 4 dx 2 4 10 0 20. 1 1 Y=x2 0 1 x Вычислим объем V тела. z x 1 2 1 V dx 4 0 1 4 x 2 0 1 2 y o 1 1 2 3 2 2 2 (1 4 x y )dy (1 4 x ) dx 30 2 2 Приложение двойных интегралов к задачам механики Масса плоской пластинки n М n ( xi , yi ) i . y pi i 1 При n M ( x, y )d D σi x1 D y1 0 x Статические моменты и центр тяжести пластинки n M x( n ) yi ( xi , yi ) i , M y( n ) i 1 M x y ( x, y )d , n x (x i 1 i i, yi ) i . M y x ( x, y )d . Координаты центра тяжести My M x ( x, y)d D ( x, y)d , Mx M D S , D ( x, y)d D D xd y ( x, y)d yd D S . . Моменты инерции пластинки. Моментом инерции материальной точки Р с массой m относительно какой-либо оси называется произведение массы на квадрат расстояния точки Р от этой оси. I x y d , 2 D I y x d . 2 D I ( x y )d I x I y D 2 2 Вычисление площади поверхности. z zi f ' x (i ,i )( x i ) f ' y ( i ,i )( y i ) z n lim diam 0 i 1 X=f(x;y) i y D S i x Si i cos i z i или S i i cos i Mi 0 y S i x Pi cos i 1 1 f ' (i ,i ) f ' (i ,i ) 2 x 2 y Следовательно: i 1 f ' (i ,i ) f ' (i ,i )Si 2 x 2 y n lim 1 diamS i 0 i 0 D 2 f ' x (i ,i ) 2 f ' y (i ,i )Si 2 dz dz 1 dxdy dx dy 2 Если x ( y , z ) или y ( x, z ), 2 D' D '' dx dx 1 dydz, dy dz 2 2 2 dy dy 1 dxdz. dx dz то Вычислим поверхность σ сферы При x2 + y2 ≤ R2, 1 2 R R R2 x2 R2 x2 dy dx 2 2 2 R x y R