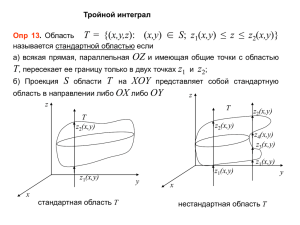
Тройной интеграл

Тройной интеграл
Лекция 9
Трехмерная область
Пусть в пространстве задана некоторая
область V, ограниченная замкнутой
поверхностью G. Пусть в области V и на
её границе определена некоторая
непрерывная функция u=f(x,y,z), где
(x,y,z) – прямоугольные декартовы
координаты точки области. Например,
если f(x,y,z)≥0, то эту функцию можно
считать плотностью распределения
некоторого вещества в области V.
Составление интегральных
сумм
Разобьём эту область V произвольным
образом на элементарные ячейки vi с
объёмами vi (i=1, 2, …, n). В каждой такой
ячейке выберем произвольную точку Mi,
вычислим значения функции в этих точках и
составим
интегральную сумму
n
 f ( M i ) v i . .
i 1
Определение
Назовём диаметром области
максимальное расстояние между двумя
точками области, лежащими на границе.
Устремим максимальный диаметр ячеек
к нулю и перейдём к пределу в
интегральных суммах .
Определение
Если существует конечный предел
интегральных сумм при условии, что
максимальный диаметр ячеек
стремится к нулю, не зависящий ни от
разбиения области V на элементарные
ячейки, ни от выбора точек Mi, то этот
предел называется тройным
интегралом по области V от функции
f(x,y,z) и обозначается  f ( x, y, z )dv.
v
Правильная трехмерная
область
Пусть пространственная область V,
ограниченная замкнутой поверхностью G,
удовлетворяет условиям:
1) всякая прямая, параллельная оси Oz,
проведённая через внутреннюю точку
области V, пересекает поверхность G в двух
точках;
2) вся область V проектируется на плоскость
Oxy в правильную область D.
Тогда область V мы будем называть
правильной трёхмерной областью.
Вычисление тройного
интеграла
Если область имеет
вид как на рисунке,
то тройной интеграл
по такой области
вычисляют по
формуле
 f ( x, y, z)dxdydz =
v
z2 ( x, y )
D dxdy z (x, yf) ( x, y, z )dz
1
Вычисление тройного
интеграла
Пример 1.
Вычислить
dxdydz
,
3

(1  x  y  z )
V
где V ограничена
плоскостями
x  y  z  1,
x=0, y=0, z=0.
Решение.
1 x  y
dxdydz
V (1  x  y  z)3  D dxdy
1
1
  
2 D (1  x  y  z ) 2
1 x
1 x  y
0

0
d ( x  y  z  1)

3
(1  x  y  z)

1 1
1
dxdy 
dxdy     
2
2 D 4
(1  x  y) 
1 x
1

1
1
1 y
1 
dy     
 dx 
   dx   
2
2 0 0  4 (1  x  y) 
2 0  4 1 x  y  0
1
1
1 1 x 1
1 
  
 
dx 
2 0 4
2 1 x 
1
1
 1 (1  x) 1 1

 
 

x

ln(
1

x
)
 8

2
4
2

0
2
1
1 1 1
5
 ln 2    ln 2  .
2
4 16 2
16
Тройной интеграл в
цилиндрических координатах
При переходе от декартовых координат
к цилиндрическим по формулам
x=rcosφ, y=rsinφ, z=z тройной интеграл
по области V преобразуется к виду
 f ( x, y, z)dxdydz
V

 f (r cos, r sin , z)rddrdz,
V
где rddrdz - это элемент объёма dv в
цилиндрических координатах.
Объем тела
В декартовых координатах объем тела
равен
V   dxdydz
V
Объем тела
Общая формула для вычисления
объема (независимо от системы
координат) имеет вид
V   dv
V
Объем тела
Объём пространственной области V в
цилиндрических координатах
V   rddrdz
V
Найти объем тела
Вычислить объём
тела, ограниченного
поверхностями
yx ,
z  y,
2
z  y  2.
Решение
Найдём линию пересечения плоскостей,
ограничивающих тело сверху и снизу.
Очевидно, это y=1.
2 y
2 y
V   dxdydz   dxdy  dz   z
V
D
1
y
y
D
dxdy   (2  2 y)dxdy 
D
y
1
1
 2 (1  y)dy  dx  2 (1  y)  x  y dy  2 (1  y)  2 y dy 
y
0
 y
0
0
1
 4
0


2
2
y  y dy  4 y  y
5
3
3
3
2
5
2
1

16
  .

 0 15
Найти объем тела
Вычислить объём
тела, ограниченного
сферой
x 2  y 2  z 2  4a 2
и параболоидом
x 2  y 2  3az
(внутри
параболоида).
Решение
Вычислим объём тела, переходя к
цилиндрическим координатам. Для
этого запишем уравнения поверхностей
в цилиндрических координатах:
2
2
2
2
r  z  4a , 3az  r. Очевидно,
поверхности пересекаются при z= a .
Вычислим теперь объём тела.
Подставляя z= a в одно из уравнений
системы, получим r  a 3.
4 a r
2
V   rddrdz   rddr
V
D
 dz   z
2
D
r
3a
2
 2 2 r 
   4a  r  rddr   d
3a 
D
0
2
4 a 2 r 2
2
a 3

0
rddr 
r2
3a

r 
2
2
 r 4a  r  dr 
3a 

2
a 3 3
 1a 3

r
 2    4a 2  r 2 d 4a 2  r 2   
dr  
 2

3
a
0
0


3
 2
2
2 2 2 r
    4a  r 
3  4a
 3


4
a 3

2 2 32 2 2 32
   a  4a 

3
3
0

a 3   2 16


a
4
3  4a
3
3
 
 
2 3 3 3 19 3

a 
a  a .
3
2
6