Вопрос 2
реклама

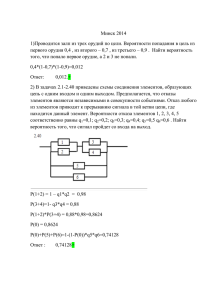
Вопрос 2 Свойства двойного интеграла 1) Пусть f(x,y) >0 в области D. Тогда: ∬𝐷 f(x, y)dxdy = 𝑉𝑇 ,Где 𝑉𝑇 – объем тела Т, ограниченного снизу областью D, а по бокам – цилиндрической поверхностью 2) Если f(x,y) = 1 по области D, то ∬𝐷 1dxdy = 𝑆𝐷 , Где 𝑆𝐷 – площадь области D 3) ∬𝐷 (𝑐1 𝑓1 (x, y) + 𝑐2 𝑓2 (x, y))dxdy = 𝑐1 ∬𝐷 𝑓1 (x, y)dxdy + 𝑐2 ∬𝐷 𝑓2 (x, y)dxdy 4) D = D1 υ D2 ∬𝐷 (𝑓1 (x, y) + 𝑓2 (x, y))dxdy = ∬𝐷1 𝑓1 (x, y)dxdy + ∬𝐷2 𝑓2 (x, y)dxdy 5) f(x,y) ≥0 ∬𝐷 f(x, y)dxdy ≥ 0 6) f2(x,y) ≥f1(x,y) в области D ∬𝐷 f2(x, y)dxdy ≥ ∬𝐷 f1(x, y)dxdy 7) D: m ≤ f(x,y) ≤ M, где m,M=const 𝑚𝑆𝐷 ≤ ∬𝐷 f(x, y)dxdy ≤ M 𝑆𝐷 8) Теорема о среднем Если в каждой точке замкнутой области D функция f(x,y) непрерывна, то тогда в области D найдется такая средняя точка Р(Хр,Ур), для которой будет выполнено соотношение: ∬𝐷 f(X, Y)dxdy = 𝑓(𝑋𝑝, 𝑌𝑝)𝑆𝐷