A y - Reshaem.Net
advertisement
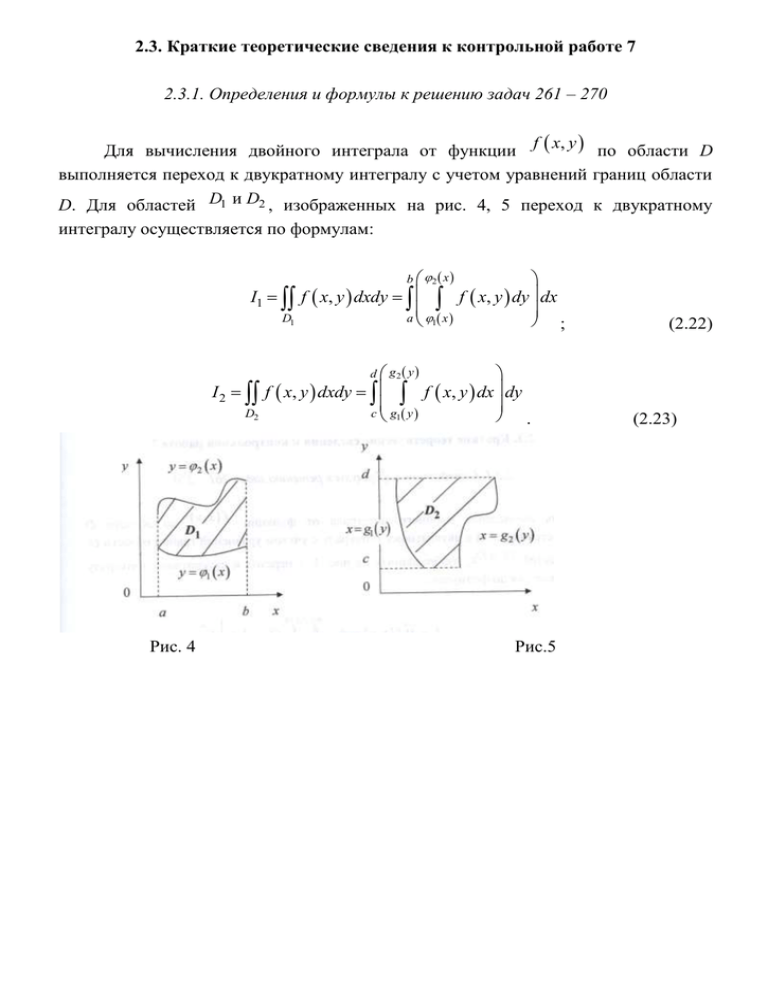
2.3. Краткие теоретические сведения к контрольной работе 7 2.3.1. Определения и формулы к решению задач 261 – 270 Для вычисления двойного интеграла от функции f x, y по области D выполняется переход к двукратному интегралу с учетом уравнений границ области D. Для областей D1 и D2 , изображенных на рис. 4, 5 переход к двукратному интегралу осуществляется по формулам: I1 D1 I 2 D2 Рис. 4 b 2 x f x, y dxdy f x, y dy dx a 1 x ; (2.22) d g2 y f x, y dxdy f x, y dx dy c g1 y . Рис.5 (2.23) y 3 y 3 x2 D y 2x 2 1 x Рис. 6 0 Для примера вычислим двойной интеграл I 2 x xy dxdy D по области D, 2 ограниченной линиями x 0; y 2 x; y 3 x и изображенной на рис. 6. По формуле (2.22) найдем: 0 1 3 x 2 I 0 2x 2 x xy dy dx . Вычисление начнем с внутреннего интеграла по у, при этом с величиной х обращаемся как с константой: 1 3 x 2 y2 I 2 xy x 2 0 2x 1 пределы интегрирования dx 3 x 2 и 2 x подставим вместо у 1 2x 3 x2 x 3 x2 2 0 2 1 2 2 x 2 x x 2 x dx 2 1 1 9 1 1 3 6 x 2 x3 x 3x3 x5 4 x 2 2 x3 dx x 4 x 2 3x3 x5 dx 2 2 2 2 0 0 1 3 x2 x3 x 4 1 x6 3 4 3 1 1 4 3 0 3 4 2 6 0 4 3 4 12 12 2 2 . При решении задач 261 – 270 используем следующий геометрический факт: двойной интеграл f x, y dxdy D при f x, y 0 в области D равен объему тела с основанием D, ограниченного сверху поверхностью z f x, y и боковой цилиндрической поверхностью с образующими, параллельными оси Oz и направляющей, которая является границей области D. З а д а ч а 12. Вычислить объем тела, ограниченного поверхностями z 0, y 2 x, y x, y 2, z 15 y 2 . Р е ш е н и е. Заданное тело Т представлено на рис. 7 «криволинейной» призмой OABO1 A1B1 . Снизу тело Т ограничено областью D – частью плоскости z = 0 (или хОу). Плоские боковые поверхности OBВ1О1, OAA1O1, ABB1 A1 − соответственно части плоскостей y x; y 2 x; y 2 . Сверху тело Т ограничено поверхностью O1 A1B1 – частью параболического цилиндра z 15 y 2 . z 15 C1 O11 1 z 15 y 2 Область D A1 O2 B1 y 2x y C2 A B y=2 0) С D 1 2 B x yx y2 y A 2 0 1 2 x 0 Рис. 7 Рис. 8 2 Поясним построение поверхности О1С1С2О2. Уравнение z 15 y не содержит переменной х. Рассмотрим его на плоскости уОz, где оно определяет параболу (линия O1C1 – часть этой параболы). Переместим эту параболу вдоль оси Ох и получим цилиндрическую поверхность O1C1C2O2 . Объем тела Т равен двойному интегралу: V z x, y dxdy 15 y 2 dxdy D D . Область D изображена на рис. 8. Расставим пределы интегрирования и y V 15 y 2 dx dy 0 1y . 2 получим двукратный интеграл При вычислении внутреннего интеграла по х с переменной у обращаемся как 2 с константой: 2 V 15 y 0 2 x y y 2 2 dy 0 2 y 1 15 15 y y dy y y 3 dy 2 2 2 0 2 2 15 y 2 1 y 4 15 1 22 24 15 2 13 8 2 2 2 4 0 4 ед. куб. 1 1 SD h AB 2 1 1 2 2 Выполним проверку. Площадь основания призмы . V 13 hcp 13 S 1 D Значит, средняя высота призмы , что визуально согласуется с чертежом. 2.3.2. Определения и формулы к решению задач 271 – 280 Работа силового векторного поля F X x, y i Y x, y j на дуге равна криволинейному интегралу по дуге от функций X x, y , Y x, y : . (2.24) B A 0 A X x, y dx Y x, y dy y y = f(x) xA Если xB уравнением dy f x dx x дуга АВ линии y f x (рис. задана 9), то и от криволинейного интеграла легко перейти к обычному определенному интегралу: Рис. 9 xB X x, y dx Y x, y dy X x, f x Y x, f x у AB у=3 3 x = 1С . (2.25) З а д а ч а 13. Вычислить работу dy = 0 В силового поля F 3x 2 y i 3xyj при обходе против часовой стрелки треугольного контура с вершинами dx= 0 y= x +1 A A 1; 2 , B 2; 3 , C 1; 3 . dy = dx 2 xA Р е ш е н и е. 0 1 2 х Заданный контур , составленный сторонами треугольника ABC , изображен на рис. 10. Найдем уравнение стороны АВ, используя уравнение прямой, проходящей через две заданные точки: Рис. 10 x xA y yA , xB x A y B y A x 1 y 2 , 2 1 3 2 y 2 x 1 или По формуле (2.24) получим y x 1. (3x 2 y)dx 3xydy. Разобьем этот интеграл по замкнутому контуру на три интеграла, соответствующих отрезкам АВ, ВС, СА: A B C A A B C 3x 2 y dx 3xydy 3x 2 y dx 3xydy 3x 2 y dx 3xydy . Учтем, что на отрезке АВ y x 1 , dy ydx 1 dx , х изменяется от 1 до 2; ВС y 3 , dy ydx 0 dx 0 , х изменяется от 2 до 1; СА x 1 , dx 0 , у изменяется от 3 до 2. Тогда 2 1 1 2 A 3x 2 x 1 dx 3x x 1 dx 3x 2 3 dx 3x 3 0 2 2 1 2 2 3 3 1 2 y 0 3 1 y dy 3x 2 x 2 3x 3x dx 3x 6 dx 3 у dy 3 2 1 2 1 2 x2 x2 x3 y2 2 2 x 3 3 6 x 3 2 3 2 2 3 1 2 3 3 3 3 22 2 2 23 12 2 1 13 12 6 1 22 6 2 22 32 2 2 2 2 12 3 27 6 3 3. 2 2 Задачи Контрольная работа 7 Кратные и криволинейные интегралы З а д а ч а 262.С помощью двойного интеграла вычислить объем тела ограниченного заданными поверхностями. 262. z 0; y x; y 4 x; y 3; z 20 y 2 . З а д а ч а 272. Вычислить работу силового поля F X x; y i Y x; y j при обходе против часовой стрелки треугольного контура с вершинами A xA ; y A , B xB ; yB , C xC ; yC .. 272. F 3x y i 2 xy j , A 1;1 , B 3;1 , C 2; 2 .