Построение графиков функций (презентация)
реклама

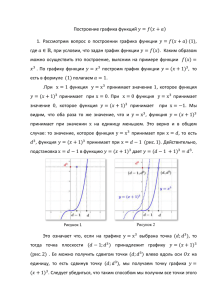
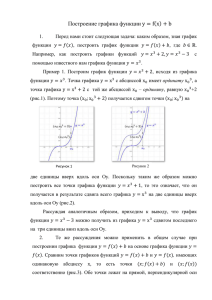
Построение графиков функций Зная график некоторой функции, можно с помощью геометрических преобразований построить график более сложной функции. 8 7 6 Рассмотрим график функции y=x2 . Выясним как можно построить графики функций вида y=(x-m)2 и y=x2+n. у = х2 5 4 3 2 1 -10 -8 -6 -4 -2 2 -1 -2 4 Из графика функции у = х2 можно получить график функции y=(x - m)2 с помощью параллельного переноса вдоль оси Ох на m единиц вправо, если m > 0, или влево, если m<0. График функции y=(x - m)2 - парабола с вершиной в точке (m; 0). Этот вывод допускает еще большее обобщение: график функции y=f(x - m) можно получить из графика функции y=f(x) с помощью параллельного переноса вдоль оси Ох на m единиц вправо, если m > 0, или влево, если m<0. Пример 1. Построим график функции y=(x - 2)2, опираясь на график функции y=x2 (щелчок мышкой). График функции y=(x - 2)2 можно получить из графика функции y=x2 путем сдвига всех его точек вправо на 2 единицы (щелчок мышкой). 9 8 7 6 5 у = х2 4 3 2 2 у = (х - 2) 1 -10 -8 -6 -4 2 2 -2 -1 4 6 8 0 График функции y=(x + 3)2 также может быть получен из графика функции y=x2, но сдвигом не вправо, а влево на 3 единицы. 8 7 у = х2 6 5 4 3 у = (х 2 + у = (х 2 - 2) 3) 2 1 -8 -6 -4 -2 2 4 6 8 -1 х = - 3 х = 2 -2 -3 -4 Хорошо видно, что осями симметрии графиков функций y=(x - 2)2 и y=(x - 3)2 являются соответственно прямые х = 2 и х = - 3. Чтобы увидеть графики, щелкни мышкой Зная график функции y=x2, можно построить график функции y=x2 +n с помощью сдвига вдоль оси Оy первого графика вверх на n единиц, если n>0, или вниз на |n| единиц, если n<0. Графиком функции y=x2 +n является парабола с вершиной в точке (0; n). Обобщение: график функции y=f(x)+n можно получить из графика функции y=f(x) сдвига графика функции y=f(x) вдоль оси Оу на n единиц вверх , если n>0, или вниз, если n>0. Страница отображается по щелчку Пример 2. Построим график функции y = x2 +1, опираясь на график функции y=x2 . 8 График функции y=x2 + 1 можно получить из графика функции y=x2 путем сдвига всех его точек вверх (вдоль оси Оу) на 1 единицу 7 2 ух = + 1 6 5 4 (щелчок мышкой). 3 2 1 у = х2 1 -10 -8 -6 -4 -2 2 -1 -2 4 График функции y=f(x - m) + n может быть получен из графика функции y=f(x) с помощью последовательно выполненных двух параллельных переносов: сдвига вдоль оси Ох на m единиц вправо, если m > 0, или влево, если m<0, и сдвига вдоль оси Оу на n единиц вверх , если n>0, или вниз, если n<0. Графиком функции y=(x - m)2 + n является парабола с вершиной в точке (m;n). Пример 3. Построить график функции у = (х+ 3)2 + 2 8 7 График функции у = (х+ 3)2 + 2 можно получить из графика функции y=x2 путем сдвига всех его точек влево (вдоль оси Ох) на 2,5 единицы и вверх (вдоль оси Оу) на 2 единицы (щелчок мышкой). -10 -8 6 у = х2 5 4 3 2 2 1 -6 -4 -2,5 -2 2 -1 -2 4 Пример 4. Построить график функции у = х2 + 6х + 8 Решение. Представим трехчленх2 + 6х + 8 в виде (x - m)2 + n. Имеем 8 х2 + 6х + 8 = х2 + 2·х·3 + 32 – 1 = =(x + 3)2 – 1. 7 Отсюда у = (x + 3)2 – 1. Значит, графиком функции 6 у = х2 + 6х + 8 является парабола с вершиной в точке (- 3; - 1). 5 Учитывая, что ось симметрии параболы – прямая х = - 3, 4 строим график (по щелчку). 8 7 6 5 у = х2 3 4 2 3 2 + 6х + 8 у = х 2 1 1 -10 -10 -8 -8 -6 -6 -4 -4 --3 3 -2 2 -2 2 -1 -1 -1 -1 Постройте самостоятельно графики функций: • • • • • • • • • у = х2 + 2; у = х2 – 3; у = (х – 1)2; у = (х + 2)2; у = (х + 1)2 – 2; у = (х – 2)2 + 1; у = (х + 3)(х – 3); у = х2 + 4х – 4; у = х2 – 6х + 11. шаблон параболы у = х2 При построении графика функции вида y=(x - m)2 + n удобно пользоваться заранее заготовленным шаблоном параболы у = х2 . Далее можно сверить свои результаты с тем, что должно быть в действительности у = х2+ 28 7 6 5 4 у = х (+ 22) 3 у = х (- 2 1) 2 1 -8 -6 -4 -2 2 -1 у = х2- 3 -2 -3 -4 4 6 8 1 -15 8 у = х (- 22) + 1 у = х2- 6х + 11 6 у = х (+21) 2 4 2 -10 -5 5 10 -2 у = (х + 3)*(х - 3) у = х2+ 4х - 4 -4 -6 -8 -10 15