Тема «Построение графика функции y=f(x)+b».
реклама
Построение графика функции y = f(x) + b
1.
Перед нами стоит следующая задача: каким образом, зная график
функции 𝑦 = 𝑓(𝑥), построить график функции 𝑦 = 𝑓(𝑥) + 𝑏, где 𝑏 ∈ ℝ.
Например, как построить графики функций 𝑦 = 𝑥 3 + 2, 𝑦 = 𝑥 3 − 3
с
помощью известного нам графика функции 𝑦 = 𝑥 3 .
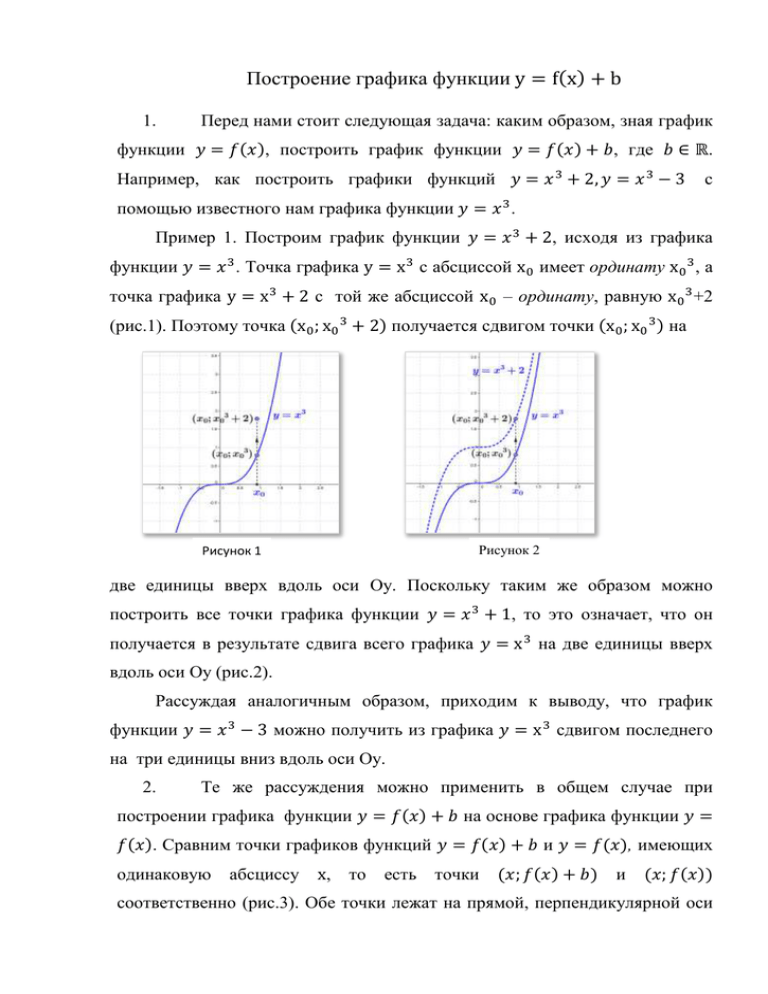
Пример 1. Построим график функции 𝑦 = 𝑥 3 + 2, исходя из графика
функции 𝑦 = 𝑥 3 . Точка графика y = x 3 с абсциссой x0 имеет ординату x0 3 , а
точка графика y = x 3 + 2 с той же абсциссой x0 – ординату, равную x0 3 +2
(рис.1). Поэтому точка (x0 ; x0 3 + 2) получается сдвигом точки (x0 ; x0 3 ) на
Рисунок 2
Рисунок 1
две единицы вверх вдоль оси Oy. Поскольку таким же образом можно
построить все точки графика функции 𝑦 = 𝑥 3 + 1, то это означает, что он
получается в результате сдвига всего графика 𝑦 = x 3 на две единицы вверх
вдоль оси Oy (рис.2).
Рассуждая аналогичным образом, приходим к выводу, что график
функции 𝑦 = 𝑥 3 − 3 можно получить из графика 𝑦 = x 3 сдвигом последнего
на три единицы вниз вдоль оси Oy.
2.
Те же рассуждения можно применить в общем случае при
построении графика функции 𝑦 = 𝑓(𝑥) + 𝑏 на основе графика функции 𝑦 =
𝑓(𝑥). Сравним точки графиков функций 𝑦 = 𝑓(𝑥) + 𝑏 и 𝑦 = 𝑓(𝑥), имеющих
одинаковую
абсциссу
x,
то
есть
точки
(𝑥; 𝑓(𝑥) + 𝑏)
и
(𝑥; 𝑓(𝑥))
соответственно (рис.3). Обе точки лежат на прямой, перпендикулярной оси
Ox, причем точка (𝑥; 𝑓(𝑥) + 𝑏) лежит выше точки (𝑥; 𝑓(𝑥)), если
𝑏 –
положительное число, и ниже этой точки, если 𝑏 – отрицательное число.
Расстояние между ними составляет |𝑏| единиц.
Рисунок 3
Из вышесказанного вытекает следующий способ построения графика
функции y = f(x) + b из графика функции y = f(x):
𝒇(𝒙)
𝒇(𝒙) + 𝒃
График функции 𝒚 = 𝒇(𝒙) + 𝒃 получается
сдвигом графика функции 𝒚 = 𝒇(𝒙) вдоль
оси ординат Oy на |𝒃| единиц.
Направление сдвига зависит от знака числа 𝐛:
график сдвигается вверх, если 𝐛 > 𝟎
график сдвигается вниз, если 𝐛 < 𝟎
3. Область определения функции y = f(x) + b совпадает с областью
определения функции y = f(x), поскольку значения функции y = f(x) + b можно
вычислить в тех только и только тех точках, в которых определена функция y =
f(x). Мы видим это в частности на примерах преобразования графиков функций,
изображенных на рисунках 4 и 5. Из рассмотрения этих же примеров можно
сделать вывод, что области значений функций 𝑦 = √𝑥 + 0,5
различаются. Так же как и функций 𝑦 =
1
𝑥
1
и 𝑦 = − 2.
𝑥
и 𝑦 = √𝑥
Рисунок 5
Рисунок 4
Напомним, что область значений функции получается в результате
проекции графика на ось ординат. По рисунку 6 можно определить, что
область значений функции y = f(x) + 4 является результатом сдвига области
Рисунок 6
значений функции y = f(x) вдоль оси Oy на то же число единиц, что и сам
график, то есть на 4 единицы вверх. Проекция графика сдвигается вместе с
ним. Поэтому, если 𝐸(𝑓) представляет собой отрезок [−2,5; 0,5] (рис.6), то
𝐸(𝑓 + 4) – это отрезок [−2,5 + 4; 0,5 + 4], то есть [1,5; 4,5].
Упражнения
1. Постройте график функции.
𝑦 = |𝑥| + 1
𝑦 = 𝑥3 + 2
2.
𝑦 = √𝑥 − 1
𝑦={
𝑥 2 − 1, если x < 0
𝑥 2 + 1, если x ≥ 0
На рисунке изображен график функции
схематически график функции y = f(x) + b.
y = f(x).
Начертите
b=1
b=-2
3. Найдите область значений функции y = f(x) + b, если известна область
значений функции y = f(x)
𝑬(𝒇)
𝒃
(−7; −2)
6
(−∞; 1]
-1
(−∞; −2) ∪ (2; ∞)
3
(−∞; ∞)
-4
(−6; 2) ∪ (2; 3)
5