Тема «Построение графика функций y=f(x+a)».
реклама
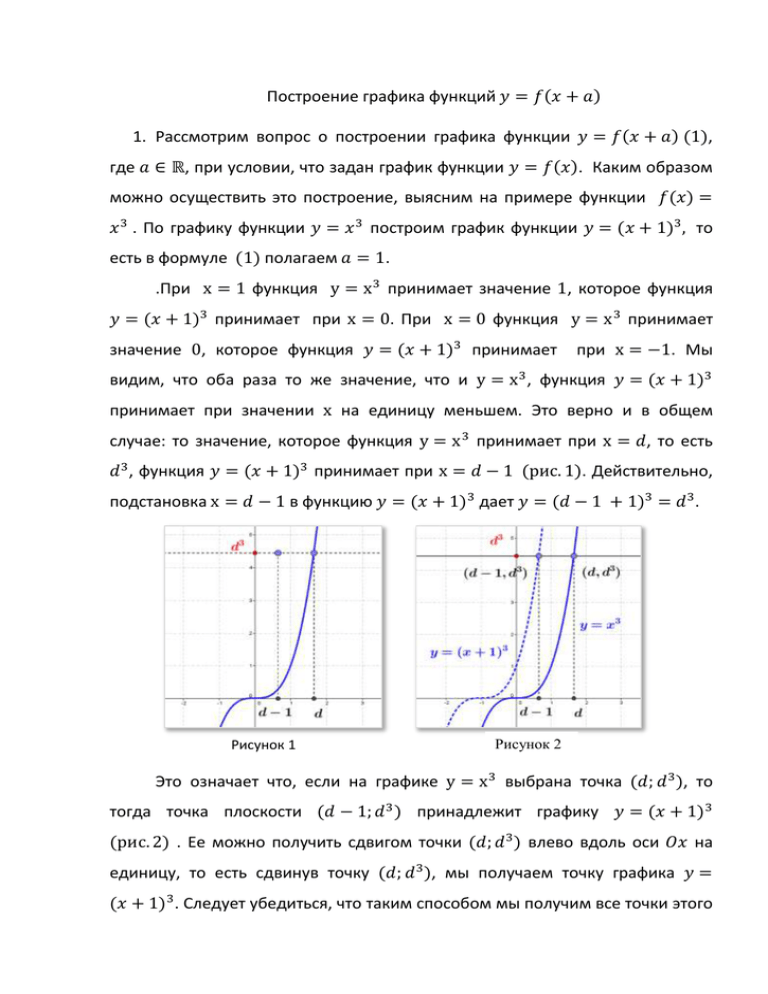
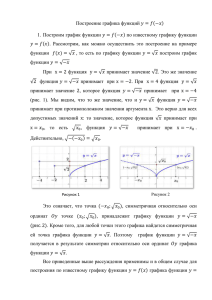
Построение графика функций 𝑦 = 𝑓(𝑥 + 𝑎) 1. Рассмотрим вопрос о построении графика функции 𝑦 = 𝑓(𝑥 + 𝑎) (1), где 𝑎 ∈ ℝ, при условии, что задан график функции 𝑦 = 𝑓(𝑥). Каким образом можно осуществить это построение, выясним на примере функции 𝑓(𝑥) = 𝑥 3 . По графику функции 𝑦 = 𝑥 3 построим график функции 𝑦 = (𝑥 + 1)3 , то есть в формуле (1) полагаем 𝑎 = 1. .При x = 1 функция y = x 3 принимает значение 1, которое функция 𝑦 = (𝑥 + 1)3 принимает при x = 0. При x = 0 функция y = x 3 принимает значение 0, которое функция 𝑦 = (𝑥 + 1)3 принимает при x = −1. Мы видим, что оба раза то же значение, что и y = x 3 , функция 𝑦 = (𝑥 + 1)3 принимает при значении x на единицу меньшем. Это верно и в общем случае: то значение, которое функция y = x 3 принимает при x = 𝑑, то есть 𝑑 3 , функция 𝑦 = (𝑥 + 1)3 принимает при x = 𝑑 − 1 (рис. 1). Действительно, подстановка x = 𝑑 − 1 в функцию 𝑦 = (𝑥 + 1)3 дает 𝑦 = (𝑑 − 1 + 1)3 = 𝑑 3 . Рисунок 1 Рисунок 2 Это означает что, если на графике y = x 3 выбрана точка (𝑑; 𝑑 3 ), то тогда точка плоскости (𝑑 − 1; 𝑑 3 ) принадлежит графику 𝑦 = (𝑥 + 1)3 (рис. 2) . Ее можно получить сдвигом точки (𝑑; 𝑑 3 ) влево вдоль оси 𝑂𝑥 на единицу, то есть сдвинув точку (𝑑; 𝑑 3 ), мы получаем точку графика 𝑦 = (𝑥 + 1)3 . Следует убедиться, что таким способом мы получим все точки этого графика. Возьмем точку графика функции 𝑦 = (𝑥 + 1)3 с абсциссой с, то есть точку (с; (с + 1)3 ). Она получается в результате сдвига влево на единицу точки (с + 1; (с + 1)3 ), которая принадлежит графику функции 𝑦 = 𝑥 3 . Таким образом, сдвинув каждую точку графика y = x 3 , то есть всю кривую целиком, влево вдоль оси 𝑂𝑥 на единицу, мы получим график функции 𝑦 = (𝑥 + 1)3 . Рассуждая аналогичным образом, можно прийти к выводу, что график функции 𝑦 = (𝑥 − 1)3 получается из графика функции 𝑦 = x 3 сдвигом последнего на единицу вправо вдоль оси Oy. Мы видим, что направление сдвига определяется знаком числа 𝑎. Если 𝑎 > 0, сдвиг происходит влево, если 𝑎 < 0 – вправо. 2. Рассуждения предыдущего пункта можно применить при построении графика функции 𝑦 = 𝑓(𝑥 + 𝑎) на основе графика произвольной функции 𝑦 = 𝑓(𝑥). Покажем, что если взять точку (х0 ; 𝑓(𝑥0 )), принадлежащую Рисунок 3 графику функции 𝑦 = 𝑓(𝑥), то тогда точка (х0 − 𝑎; 𝑓(х0)) будет принадлежать графику функции 𝑦 = 𝑓(𝑥 + 𝑎). Последнее выполняется в случае, если при 𝑥 = х0 − 𝑎 значение функции 𝑦 = 𝑓(𝑥 + 𝑎) равно 𝑓(х0 ). А это следует из равенства 𝑓((х0 − 𝑎 ) + 𝑎) = 𝑓(х0 − 𝑎 + 𝑎) = 𝑓(х0 ). Верно и обратное утверждение. Отметим, что число х0 − 𝑎 меньше числа х0 , в случае 𝑎 > 0. Если же 𝑎 < 0, то х0 − 𝑎 больше чем х0 , например, при 𝑎 = −3 получаем х0 < х0 + 3. Это означает, что точка с абсциссой х0 − 𝑎 лежит левее, чем точка с абсциссой х0 , если 𝑎 > 0, и правее ее, если 𝑎 < 0. В последнем случае удобно записать х0 − 𝑎 в виде х0 + |𝑎|. Таким образом, мы можем сформулировать следующий способ построения графика функции y = f(x + 𝑎) из графика функции y = f(x): 𝒇(𝒙) 𝒇(𝒙 + 𝒂) График функции 𝒚 = 𝒇(𝒙 + 𝒂) получается сдвигом графика функции 𝒚 = 𝒇(𝒙) оси вдоль ординат Ox на |𝒂| единиц. Направление сдвига зависит от знака числа 𝐚: график сдвигается влево, если 𝐚 > 𝟎 график сдвигается вправо, если 𝐚 < 𝟎 3. Поскольку множество значений функции является проекцией графика на ось ординат, то сдвиг вдоль этой оси графика функции 𝑦 = 𝑓(𝑥) не изменяет саму проекцию (рис.4). Это означает, что 𝐸(𝑓 + 𝑎) = 𝐸(𝑓). Рисунок 4 Однако, области определения функций в общем случае не совпадают. Область определения функции 𝑦 = 𝑓(𝑥 + 𝑎) получается в результате сдвига области определения функции 𝑦 = 𝑓(𝑥) по оси 𝑂𝑦 на то же число единиц, на которое сдвигается и сам график (рис.4). Поэтому, для функции, изображенной на рисунке 4, 𝐷(𝑓) представляет собой отрезок [7; 12], а 𝐷(𝑓 + 6) – отрезок[1; 6], поскольку 𝑎 = 6. Если 𝐷(𝑓) = 𝑅, то очевидно, что и 𝐷(𝑓 + 𝑎) = 𝑅. 4. На рисунках 5 и 6 приведены примеры построения графиков функций 𝑦 = |𝑥 + 2| и 𝑦 = √𝑥 − 3, соответственно. Рисунок 6 Рисунок 5 Пример. Построить график функции 𝑦 = √4𝑥 + 10. Решение. Поскольку √4𝑥 + 10 = √4(𝑥 + 2,5) = 2√𝑥 + 2,5, то запишем формулу функции в виде 𝑦 = 2√𝑥 + 2,5. Построим сначала график функции 𝑦 = √𝑥 + 2,5, сдвинув влево на 2,5 единицы вдоль оси 𝑂𝑥 график функции 𝑦 = √𝑥. Затем растянем график функции 𝑦 = √𝑥 + 2,5 в 2 раза вдоль оси 𝑂у. В итоге получим график функции 𝑦 = 2√𝑥 + 2,5 (рис.5). Последовательность построения графиков удобно записать в следующем виде: 𝑦 = √𝑥 ⟹ 𝑦 = √𝑥 + 2,5 2√𝑥 + 2,5 . Рисунок 5 ⟹ 𝑦= Упражнения 1. Функция 𝑦 = 𝑓(𝑥) задана графиком. Построите график функции 𝑎) 𝑓(𝑥 − 1) 𝑏) 𝑓(𝑥 + 2) 𝑐) − 𝑓(𝑥 − 1) 𝑑) 0,5𝑓(𝑥 + 2) 2. Постройте эскиз графика функции y = g(x) 𝒈(𝒙) 𝒈(𝒙) 𝒈(𝒙) |𝑥 + 2| (𝑥 − 1)3 √𝑥 + 1 (−𝑥 + 3)2 (𝑥 − 3)2 (𝑥 + 2)2 |1 − 𝑥| 1 𝑥+1 1 𝑥−1 √9𝑥 + 27 |2𝑥 − 1| (0,5𝑥 + 2)2 3. Найти область определения функции 𝑦 = 𝑓(𝑥 + 𝑎), если известна область определения функции 𝑦 = 𝑓(𝑥). 𝑫(𝒇) 𝒂 (0; 2) 6 (−∞; 1] -1 (−∞; −2) ∪ (2; ∞) 2 (−∞; ∞) -4 (−6; 0) ∪ (0; 3) -3