10 развязка инд. связи, трансформатор
реклама

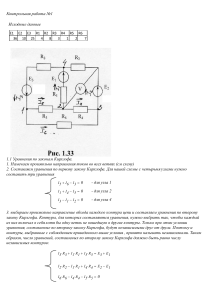
8 ЛЕКЦИЯ Развязка индуктивной связи Трансформатор 1 Развязка индуктивной связи 2 Развязка индуктивной связи применяется для ее исключения с целью упрощения расчетов и может быть доказана при помощи законов Кирхгофа в комплексной форме 3 1. Два индуктивно связанных комплексных сопротивления подходят одинаковым образом к общему узлу (d) 4 5 2. Два индуктивно связанных комплексных сопротивления подходят различным образом к общему узлу (d) 6 7 После развязки индуктивной связи для расчета цепи можно использовать любой известный метод в комплексной форме 8 Пример 9 Дано: Е Ee j J Je j Z 1 R1 jX 1 Z 2 R2 jX 2 Z R jX Z М jX М Определить: I ? 10 После развязки: 11 Используем метод эквивалентного генератора 12 Е Г U xx E J ( Z 1 Z M ) E Г e j Г Z Г (Z 2 Z M ) (Z 1 Z M ) RГ jX Г Z Г e j Г 13 I EГ ZГ Z Ie j Действующее значение тока: I EГ ( R Г R) ( X Г X ) 2 2 14 Активная мощность нагрузки Z: PI R 2 2 EГ R 2 ( R Г R) ( X Г X ) 2 f (R) 15 P Pm P f (R) 0 Rm Rm R Г2 ( Х Г Х ) 2 ; R Е Г2 Pm 2( Rm R Г ) 16 ТРАНСФОРМАТОР В ЛИНЕЙНОМ РЕЖИМЕ 17 Трансформаторы предназначены для преобразования величин переменных напряжений и токов. Простейший трансформатор – это две индуктивно связанные катушки, помещенные на ферромагнитный сердечник (магнитопровод) 18 1 + u1 1’ i2 i1 w2 w1 Ф 2 + u2 2’ Ф – магнитный поток, Вб 19 В линейном режиме магнитопровод ненасыщен или отсутствует (воздушный трансформатор) При этом индуктивности и сопротивления катушек трансформатора постоянны 20 Передача энергии из одной катушки в другую осуществляется за счет взаимной индукции и ток i2(t) согласно правилу Ленца выбирает такое направление, что катушки будут включенными встречно 21 Если пренебречь потерями энергии в магнитопроводе, то тогда схема замещения трансформатора в линейном режиме будет следующей 22 Схема замещения: 1 i1 u1 1’ М * L1 R1 * L2 R2 i 2 2 ZH u2 2’ 23 Если u1 является напряжением источника, а u2 – напряжением на пассивной нагрузке, то тогда получаем 24 Уравнения по 2 закону Кирхгофа В дифференциальной форме: di1 di2 u1 R1i1 L1 M dt dt di2 di1 0 u 2 R2i2 L2 M dt dt 25 Комплексная схема замещения: 1 U1 1’ I1 ZМ * Z1 I2 * Z2 2 U2 ZН 2’ 26 Где: Z 1 R1 jX L1 Z 2 R2 jX L2 - Полные сопротивления обмоток трансформатора Z M jX M - сопротивление взаимной индукции 27 Уравнения по 2 закону Кирхгофа в комплексной форме: U 1 R1 I 1 I 1 jX L1 I 2 jX M U R1 U L1 U M1 0 U 2 R2 I 2 I 2 jX L2 I 1 jX M U U U U 2 R2 L2 M2 Где: U2 I2 ZH 28 Из решения этих уравнений можно найти токи I1 и I2 29 Векторная диаграмма при холостом ходе ( I2=0 ): +j U1 U M2 U 2 U R1 U L1 I 1 I1e j 0 +1 30 Векторная диаграмма при коротком замыкании ( U2=0 ): 31 +j U L2 UM2 UM 1 U1 U R2 U L1 U R1 I1 I2 +1 32 Векторная диаграмма для активной нагрузки: U 2 I 2 RH 33 +j U L2 U M2 UM1 U1 U 2 U R2 U R1 I1 U L1 I2 +1 34 Векторная диаграмма для ёмкостной нагрузки: U 2 I 2 ( jX CH ) 35 +j U L2 U2 U R2 U R1 I1 U L1 U M2 I2 +1 U1 UM1 36 Схема замещения трансформатора без индуктивной связи: 1 I 1 Z1 Z M Z2 ZM ZM U1 I2 2 U2 I0 2’ 1’ I0 - ток намагничивания 37 Линейные цепи с гармоническими напряжениями и токами, содержащие трансформаторы, могут быть рассчитаны при помощи законов Кирхгофа или метода контурных токов в комплексной форме 38 Пример: I11 Z3 Е * I22 I3 ZM I2 I1 * I33 Z2 J Z1 + UJ ZH I11 39 Дано: E , J , Z1 , Z2 , Z3 , ZH Определить: I1 , I2 , I3 , UJ 40 По методу контурных токов: I11=J I22(Z2+Z3) - I33ZM - I11Z3 = E - I22ZM + I33(Z1+ZH) + I110 = 0 41 Далее находим: I1 = I11 I2 = I22 I3 = I22 – I11 UJ = E – Z3I3 42