Построение графика квадратичной функции:

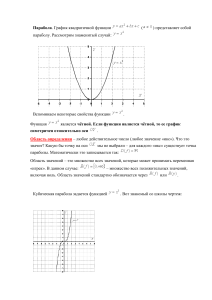
Построение графика
квадратичной функции:
у  ах
2
 вх  с
Опорные точки для построения графика
(выполни конспект в тетради)
• А х0 , у0  – вершина
параболы;
• В х1;0 и С х2 ;0 точки пересечения
графика с осью ОХ;
• Д (0;У) – точка
пересечения графика
с осью ОУ, Е 0; у1  точка симметричная
точке Д.
в
х0  
2а
Д
2
у0  у ( х0 )  ах  вх0  с  
 ах0  с
4а
2
0
Прямая х= х0 - ось симметрии параболы
Д  в  4ас
2
• Решите квадратное уравнение:
ах 2  вх  с  0
Д  в  4ас
2
х1, 2
в Д

2а
Если Д<0, то график функции не
пересекает ось ОХ. При а>0 вся парабола
расположена выше оси ОХ, а при а<0
ниже оси ОХ.
• Постройте точки параболы с абсциссами
х  0 И х  2х0
Ординаты этих точек равны с.
Д 0; с ; Е 2 х0 ; с 
В этом случае целесообразно
найти координаты ещё двух точек,
симметричных относительно оси
параболы.
Пример 1.
• Построить график функции: у  3х 2  12 х  15
• 1. Вычислим координаты вершины параболы:
в
 12
х0  

 2
2а 2 * 3
у0  ах02  с  3(2) 2  15  3
Построим точку  2;3 и проведём через неё
прямую, параллельную оси ординат – ось
симметрии параболы.
2. Решая уравнение
3х  12 х  15  0,
2
убеждаемся, что действительных
корней нет, и поэтому
парабола не пересекает ось ОХ.
Д=144-4*3*15=144-180=-36 < 0
3.Возьмём две точки на оси ОХ,
симметричные относительно точки х=-2,
например точки х=-1 и х=-3.
Вычислим значение функции в этих
точках:
у(-1) = у(-3) = 6.
Построим данные точки в системе
координат.
Найдём координаты точки
пересечения графика с осью Оу.
у(0)=с=15.
Построим точки (0;15) и
симметричную ей, относительно оси
симметрии параболы, (-4;15).
Проведём параболу через
построенные точки.
Постройте графики функций:
(выполните в тетрадях)
• 1.
у  3х  3х  1
• 2.
у  2 х  5х  2
•
2
2
Справились? Проверьте!
(5/4;-1 1/8) – ВЕРШИНА ПАРАБОЛЫ
(- ½;1 ¾) – ВЕРШИНА ПАРАБОЛЫ
По данному графику квадратичной функции выяснить её
свойства (в тетрадях).
1
2
•
СРАВНИ ПОЛУЧЕННЫЕ ДАННЫЕ С ТАБЛИЦЕЙ.
СВОЙСТВА
ФУНКЦИИ
1
2
ПРОМЕЖУТКИ ВОЗРАСТАНИЯ
И УБЫВАНИЯ ФУНКЦИИ
Х-1,5 - ; Х-1,5 - 
Х0,75 -  Х0,75 - 
ПРОМЕЖУТКИ
ЗНАКОПОСТОЯНСТВА
НАИБОЛЬШЕЕ ИЛИ
НАИМЕНЬШЕЕ
ЗНАЧЕНИЕ ФУНКЦИИ
У>0
У<0
У=0
Х0
-
Х=0
У=0 - НАИМЕНЬШЕЕ
Х=-0,5
Х=2
У=3,2 - НАИБОЛЬШЕЕ
-0,5Х2
Х-0,5
Х2
Пример 2.
свойства:
По графику функции можно определить её
• 1. Функция принимает значения у  -8 при любых
значениях х .
У=-8 – наименьшее значение функции при х=1.
(Координаты вершины параболы) .
• 2. Функция возрастает на промежутке х  1;
убывает на промежутке х  1.
• 3. Функция принимает отрицательные значения у<0
при -1<x<3; положительные у>0 при х<-1 и х>3;
нулевое значение у=0 при х = -1 и х =3
(х = -1 и х=3 –абсциссы точек пересечения графика с
осью Ох).
• 4. График функции симметричен относительно прямой
х=1.
график
У>0
У=0
У=0
Х0
У0
У<0
Подведение итогов:
Ты научился:
• 1. Строить график квадратичной функции.
• 2. Определять её свойства по готовому
графику.
Если материал усвоен не очень хорошо, то
можно ещё раз его прочитать. А если вопросов
нет, то приступай к изучению следующей
темы.