Тема урока: «Функция у = k/х и ее график» Цель урока:

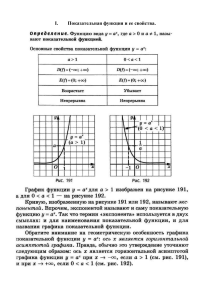
Тема урока: «Функция у = k/х и ее график»
Цель урока: «Выработать знания и умения в построении графика
обратной пропорциональности; уметь находить по
графику значение аргумента по заданному значению
функции; уметь находить по графику значение функции по заданному значению аргумента».
Ход урока
I. Повторение изученного материала.
Учащимся предлагается разгадать кроссворд, который заранее подготовлен
на доске.
Вопросы кроссворда
1. Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной. (функция)
2. Независимая переменная. (аргумент)
3. Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениям функции.(график).
4. Функция, заданная формулой y = kx + b. (линейная)
5. Каким коэффициентом называют число k? (угловым).
6. Что служит графиком линейной функции? (прямая).
7. Если k≠0, то график y = kx + b пересекает эту ось, а если k=0, то параллелен
ей. Какой буквой эта ось обозначается? (икс).
8. Слово в названии функции y = kx. (пропорциональность).
9. Функция y = x2 (квадратичная).
10. Название графика квадратичной функции. (парабола).
11. Буква латинского алфавита, которой часто обозначают функцию. (игрек).
12. Один из способов задания функции. (формула).
После того, как кроссворд разгадан, учитель задает классу вопрос: «Какие основные способы задания функции вам известны?» (Формулой, с помощью
графика или таблицы).
У доски работает ученик. Задание: заполнить таблицу №1 и таблицу №2
значений функции у = 12/х по данным значениям его аргумента.
Таблица №1
х
1
у
2
3
4
5
6
8
12
Таблица №2
х
-1
у
-2
-3
-4
-5
-6
-8
-12
Пока вызванный к доске ученик работает, весь класс отвечает на вопросы, которые выписаны на отдельной доске.
Вопросы.
Как называются следующие функции, заданные формулами:
y = kx,
y = kx + b,
y = x2, y = kx2, y = x3, y = kx3 ?
Укажите область определения следующих функций:
у=х2+8, у=1/х-7, у=4х-1/5, у=2х, у=7-5х, у=2/х, у= х3, у= -10/х.
После фронтального разбора вопросов, проверяем правильность заполнение
таблиц учеником, работающим у доски.
Следующий ученик выполняет у доски новое задание: по данным в таблице координатам (х; у) построить на координатной плоскости соответствующие точки.
Весь класс в это время занимается по таблице №3, отвечая на поставленные
учителем вопросы:
1. На каком рисунке из таблицы изображен график:
а) линейной функции; б) прямой пропорциональности;
в) квадратичной функции; г) функции вида у=kx3
2. Какой знак имеет коэффициент k в формуле вида y=kx+b, которым соответствуют графики на рис. 1, 2, 4, 5 таблицы?
3. Найдите в таблице №3 графики линейных функций, у которых угловые коэффициенты: а) равны; б) равны по модулю и противоположны по знаку.
Таблица №3
Первая часть урока заканчивается тем, что весь класс проверяет, верно ли ученик, вызванный к доске, расставил точки на координатной оси.
II. Объяснение нового материала.
Как известно всякая функция описывает какие –то процессы, происходящие в
окружающем нас мире. Рассмотрим например прямоугольник со сторонами х и
у и площадью 12см2. Известно, что ху=12см2. Но что будет, если начать изменять одну из сторон прямоугольника, допустим сторону длиной х ? Длину стороны у можно узнать из формулы у = 12/х. Если х увеличить в 2 раза, то будем
иметь у = 12/2х, т.е сторона у уменьшится в 2 раза. Если значение х увеличивать
в 3, 4, 5, … раз, то значение у во столько же раз уменьшается. Наоборот, если х
уменьшать в несколько раз, то у будет увеличиваться во столько же раз. Поэтому функцию вида у = 12/х называют обратной пропорциональностью. В общем
виде она записывается так: y=k/x , где k- константа, причем k≠0
Такие функции встречаются очень часто. В курсе физики изучается закон
Ома: I=U/R . Он гласит, что если напряжение U постоянно, то сила тока I обратно пропорциональна сопротивлению R проводника.
Как же выглядит график данной функции?
Давайте попробуем вместе сделать выводы о графике функции, вытекающие из
рассмотрения таблицы и формулы.
Вопросы и ответы.
1. Какова область определения функции у=12/х?
 Все числа, кроме 0.
2. Положительные или отрицательные значения у, если х<0, х>0?
 При х<0 имеем: у<0, при х>0 имеем у>0.
3. Как меняется переменная у с изменением х?
 При х>0: если х→0, то и у→∞, если х→∞, то у→0.
При х<0: если х→0, то и у→ -∞, если х→ -∞, то у→0
Выводы.
1. Точка (0;0) не принадлежит графику, т.е. он не пересекает ни оси Ох, ни оси
Оу.
2. График находится в I и в III координатных четвертях.
3. Плавно приближается к координатным осям в этих четвертях, причем он
подходит к осям как угодно близко.
Соединяем полученные точки и получаем график функции у=12/х. Полученная кривая называется гиперболой , что в переводе с греческого означает “прохожу через что-либо”.
Теперь рядом с графиком функции у=12/х построим графиком функции
у= -12/х. Сравнивая оба графика, учащиеся замечают, что второй занимает II и
IV координатные углы, а оба они симметричны относительно начала координат.
К тому же если график функции у=12/х отобразить симметрично относительно
оси Оу, то получится график функции у= -12/х.
Затем в классе выясняется вопрос: “Как зависит расположения графика гиперболы y=k/x от знака и от значения коэффициента k?”
III. Закрепление изученного материала
а) Заполнить таблицу значений данной функции у=8/х;
б) Выяснить вопрос о принадлежности точки, заданной своими координатами,
конкретному графику у=8/х;
в) Найти по графику значения у, если даны значения х и наоборот.
IV. Самостоятельная работа. (разноуровневоя).
Вариант 1.
Постройте график обратной пропорциональности у= -6/х с помощью табл.4
х
у
-6
=+1
-4
+1,5
-3
+2
-2
+3
1
-6
2
-3
3
-2
4
-1,5
6
-1
Вариант 2
Постройте график обратной пропорциональности у= 16/х с помощью табл.5
х
у
-16
-12
-8
-4
-2
-1
1
2
4
8
12
Вариант 3
Постройте таблицу некоторых значений функции у=10/х и ее график .
V. Домашнее задание.
Построить графики функций: у= -8/х ; у = 8/х; у = -12/х; у = 12/х
16