реклама
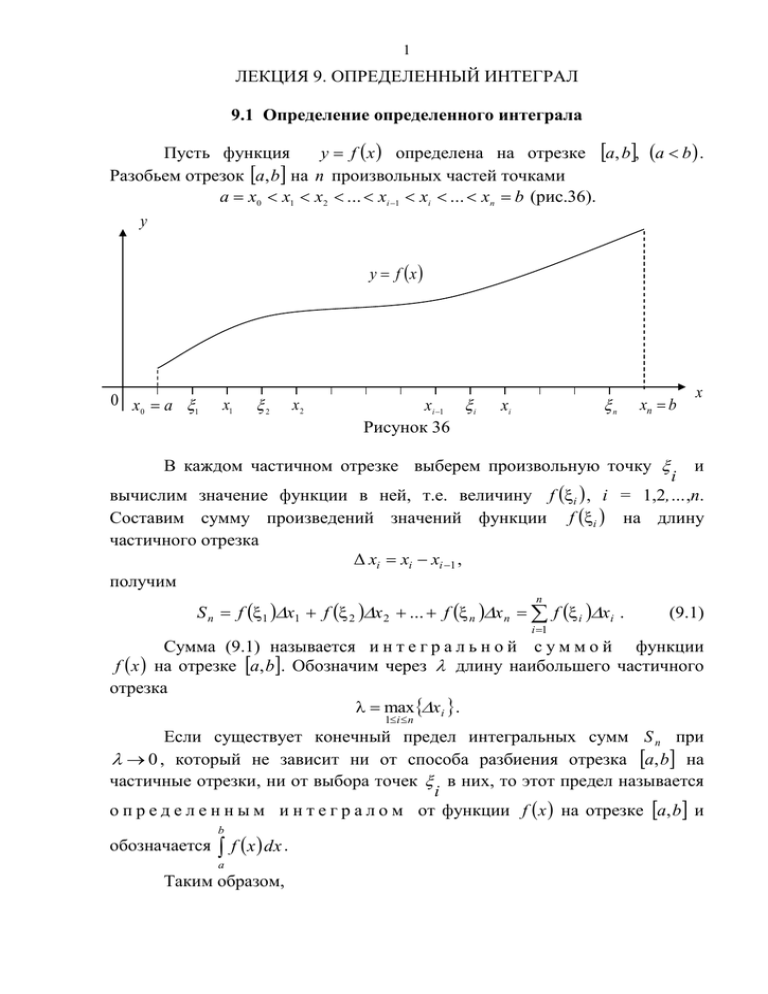
1 ЛЕКЦИЯ 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ 9.1 Определение определенного интеграла y f x определена на отрезке a, b, a b . Пусть функция Разобьем отрезок a, b на n произвольных частей точками a x0 x1 x2 ... xi 1 xi ... xn b (рис.36). y y f x 0 x a 0 1 x1 2 x2 xi 1 i Рисунок 36 n xi xn b x В каждом частичном отрезке выберем произвольную точку и i вычислим значение функции в ней, т.е. величину f i , i = 1,2,…,n. Составим сумму произведений значений функции f i на длину частичного отрезка Δ xi xi xi 1 , получим n S n f 1 x1 f 2 x 2 ... f n x n f i xi . (9.1) i 1 Сумма (9.1) называется и н т е г р а л ь н о й с у м м о й функции f x на отрезке a, b. Обозначим через длину наибольшего частичного отрезка maxx i . 1i n Если существует конечный предел интегральных сумм S n при 0 , который не зависит ни от способа разбиения отрезка a, b на частичные отрезки, ни от выбора точек в них, то этот предел называется i о п р е д е л е н н ы м и н т е г р а л о м от функции f x на отрезке a, b и b обозначается f x dx . a Таким образом, 2 b n a i 1 f i xi . f x dx lim 0 (9.2) Числа а и b называют соответственно н и ж н и м и в е р х н и м пределами интегрирования. Теорема Коши. Если функция f x непрерывна на отрезке a, b, то b f x dx существует. a Теорема. Если функция f x интегрируема на отрезке a, b, то она определенный интеграл ограничена на этом отрезке. 9.2 Основные свойства определенного интеграла 1. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный, т.е. b a a b f x dx f x dx . 2. Определенный интеграл с равными нижним и верхним пределами равен нулю, т.е. a f x dx 0 . a 3. Постоянный множитель можно выносить за знак определенного интеграла, т.е. b b a a k f x dx k f x dx , k const . 4. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме определенных интегралов от слагаемых b b b a a a f x x dx f x dx x dx . 5. Для любых чисел а , b и c имеет место равенство b 6. Если f x 0 c b f x dx f x dx f x dx . a a c x a, b , то b f x dx 0 . a 7. Если f x x x a, b , то b 8. Если m f x M b f x dx x dx . a a x a, b, a < b, то 3 b m b a f x dx M b a , a где m, M – соответственно наименьшее и наибольшее значения функции у f x на отрезке a, b. 9. Теорема о среднем. Если функция y f x непрерывна на отрезке a, b, a b , то найдется такое значение c a, b, что b f x dx f c b a . a 2 f x dx, если f x четная 10. f x dx 0 a 0, если f x нечетная a a 11. b b a a f x dx f x dx . 12. Производная определенного интеграла от непрерывной функции по переменному верхнему пределу равна значению подынтегральной функции в точке, равной верхнему пределу, т.е. x f t dt f x . a 13. Связь между неопределенным и определенным интегралами x f x dx f t dt c . a 14. Определенный интеграл не зависит от обозначения переменной интегрирования b b b a a a f x dx f t dt f z dz . 9.3 Формула Ньютона – Лейбница Теорема. Если функция y f x непрерывна на отрезке a, b и F x – любая ее первообразная на отрезке a, b , то имеет место формула b f x dx F b F a . a Эта формула называется ф о р м у л о й Н ь ю т о н а – Л е й б н и ц а и ее можно записать в виде b b a a f x dx F x F b F a . 4 Примеры. x3 1. x dx 3 2 3 2 3 2 2. sin xdx cos x cos cos 0 1 1 2 . 0 0 2 3. 2 dx ln x ln 2 ln 1 ln 2 . x 1 1 3 4. 33 2 3 19 . 3 3 3 e 0 x dx e x 3 e 3 1. 0 9.4 Замена переменной в определенном интеграле Теорема. Пусть f x непрерывная функция на отрезке a, b . Если: 1) функция x t и t непрерывны при t , ; 2) множеством значений функции x t при t , является отрезок a, b ; 3) a и b , то b a f x dx f t t dt . Эта формула называется ф о р м у л о й з а м е н ы п е р е м е н н о й в определенном интеграле. Замечания. 1. Часто вместо подстановки x t применяют подстановку t g x . 2. При замене переменной нужно поменять пределы интегрирования. 3. При вычислении определенного интеграла методом замены переменной не надо возвращаться к старой переменной. 1 Пример 9.1. Вычислить 1 x 2 dx . 0 1 Решение. x sin t dx cos tdt 2 2 2 2 1 x dx при x 0, t 0 1 sin t cos t dt cos2 t dt 0 при x 1, t 2 2 0 2 0 1 1 cos2t dt 1 t 1 sin 2t 1 1 sin sin 0 . 20 2 2 0 2 2 2 4 5 9.5 Формула интегрирования по частям в определенном интеграле Теорема. Если функции U U x и V V x имеют непрерывные производные на отрезке a, b , то справедлива формула: b b a a U dV UV Доказательство. Т.к. b V dU . a UV U V U V x a, b, то UV является первообразной для U V U V , тогда b b a a U V U V dx UV или b b V U dx U V dx UV a a b , a отсюда b b a a U dV UV b V dU . a 2 Пример 9.2. Вычислить xe x dx . 1 Решение. Ux 2 dU dx x xe dx dV e x dx 1 V e dx e x xe x 2 1 2 e dx 2e e e x 2 1 x e Пример 9.3. Вычислить x ln xdx . 1 Решение. U ln x dx dU e x x ln xdx dV xdx 1 x 2 e 1 e 2 dx ln x x 2 1 21 x x2 V xdx 2 2 2 e 2 e 1 x e e2 1 e2 1 1 2 0 e 1 . 2 2 2 1 2 4 4 4 4 4 x 2 1 2e2 e e 2 e e 2 .





![Задание 7. Поиск значения обратной ... Создайте класс, содержащий метод, который для переданной на вход произвольной... [a,b]](http://s1.studylib.ru/store/data/004633031_1-8806371c9708a533a3c0570912606841-300x300.png)