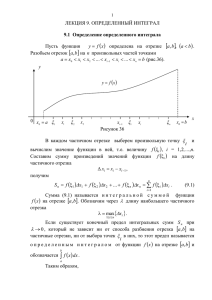
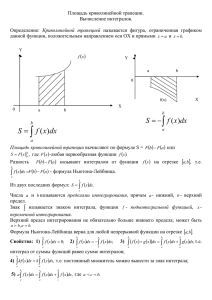
Лекция 6. Интеграл Римана. 1. Понятие интеграла Римана. Необходимое условие интегрирования. ОПР. На отрезке a; b расположены точки x0 a, x1 , x2 ,..., xn b . Говорят, что они задают разбиение x0 , x1 ,..., xn отрезка a; b c параметром max xk , где xk xk xk 1 . k ОПР. Для любого набора 1 , 2 ,..., n точек k xk 1 ; xk выражение n S ( f , ) f ( k )xk называется интегральной суммой Римана. k 1 ОПР. Интегралом Римана функции y f (x) на отрезке a; b называют число равное b J f ( x)dx lim S ( f , ) . 0 a т.е. 0 : , и S ( f , ) J . Функция, для которой существует интеграл Римана, называется интегрируемой. Существуют функции, не имеющие интеграла, например, на отрезке 0,1 функция 1, x Q f ( x) не имеет интеграла, поскольку существуют разбиения и с как 0, x R / Q угодно малым значением , для которых S ( f , ) =1 и S ( f , ) =0. ТЕОРЕМА 1. (необходимое условие существования интеграла) b Если существует интеграл Римана J f ( x)dx , то функция y f (x) ограничена на a отрезке a; b . ДОК. Из условия существования интеграла следует ограниченность интегральных сумм Римана: M : S ( f , ) M для любых разбиений с достаточно малым и любым . Фиксируем одно из таких разбиений ~ . Пусть функция y f (x) неограниченна на a; b . Тогда она неограниченна хотя бы на одном из отрезков разбиения ~ , например, на a; x . Изменяя только 1 можно добиться как угодно больших значений первого слагаемого 1 n интегральной суммы S ( f , ) f (1 )x1 f ( k )xk . k 2 ОПР. Разбиение отрезка x0 , x1 ,..., xp называется последующим по отношению к x0 , x1 ,..., xn , обозначение , если точки разбиения содержатся в множестве точек разбиения . Следующие два утверждения подготовят к доказательству достаточного условия интегрируемости функции. ЛЕММА 1. Если - разбиение отрезка a; b , для которого , то для любого последующего разбиения выполняется неравенство S ( f ) S ( f ) f ( )b a . Здесь f ( ) sup x1 , x2 X , x1 x2 f ( x1 ) f ( x2 ) - колебание функции f ( x) на множестве X a; b . ДОК. Выберем любой отрезок xk 1 ; xk разбиения . В разбиении на этом отрезке могут появиться новые точки xk 1,1 , xk 1, 2 ,..., xk 1,m и новые k ,1 , k , 2 ,... k ,m . Тогда изменение интегральной суммы можно оценить с помощью функции колебания: k f ( k , j )xk , j f ( k )xk f ( k , j f ( k ) xk , j m m j 1 j 1 m k f ( k , j ) f ( k ) xk , j f ( )xk . j 1 Наконец, S ( f ) S ( f ) n n n k 1 k 1 k 1 k k f ( )xk f ( )b a . ЛЕММА 2 Для двух произвольных разбиений и отрезка a; b , для которых и , справедлива оценка S ( f ) S ( f ) 2 f ( )(b a) . ДОК. Рассмотрим разбиение , в котором участвуют все точки из разбиения и . Тогда , и . По лемме 1 S ( f ) S ( f ) S ( f ) S ( f ) S ( f ) S ( f ) 2 f ( )(b a) . Интересно следствие из доказанной оценки, получаемое предельным переходом при 0 : b f ( x)dx S ( f ) f ( )(b a) для любого : и любого . a Следующая теорема выражает достаточное условие интегрируемости. ТЕОРЕМА 2. Всякая функция, непрерывная на отрезке a; b , интегрируема на a; b . ДОК. Используя критерий Коши достаточно доказать, что 0 : , : , S ( f ) S ( f ) . Действительно, из условия непрерывности функции y f (x) следует, что существует . Тогда , : , с учетом леммы 2 2(b a) S ( f ) S ( f ) 2 f ( )(b a) . 0 , для которого f ( ) 2. Свойства определенного интеграла. А. Свойство линейности. Если функции y f (x) , y g (x) интегрируемы на отрезке a; b , b b b b b a a a a a f ( x) g ( x)dx f ( x)dx g ( x)dx и kf ( x)dx k f ( x)dx для любого k R . B. Аддитивность интеграла по множеству. Если функция y f (x) интегрируема на отрезках a; c и c; b , то она интегрируема на их объединении a; b a; c c; b . Действительно, любое разбиение : отрезка a; b порождает два разбиения , : , отрезков a; c и c; b соответственно. Тогда S ( f ) S ( f ) S ( f ) и, переходя к пределу при 0 , получим b c b a a c f ( x)dx f ( x)dx f ( x)dx C. Интегрирование неравенства. Если функции y f (x) , y g (x) интегрируемы на отрезке a; b и f ( x) g ( x), x a; b , то b b a a f ( x)dx g ( x)dx . Действительно, S ( f ) S ( g ) и знак неравенства не меняется после предельного перехода. Если неотрицательная непрерывная функция хотя бы в одной точке отрезка b положительна, то f ( x)dx 0 . a D. Оценка определенного интеграла. b Если m inf f ( x) и M sup f ( x) , то m(b a) f ( x)dx M b a . xa ;b xa ;b a Действительно, g ( x) m f ( x), x a; b и по свойству C b b a a m(b a) mdx f ( x)dx . Аналогично, f ( x) g ( x) M , x a; b и по свойству C b b a a f ( x)dx Mdx M (b a) . E. Теорема о среднем для определенного интеграла. Если функция y f (x) непрерывна на отрезке a; b , то существует c a; b, для которого b f ( x)dx f (c)(b a) . a Действительно, по свойству D: b 1 f ( x)dx m; M , но по теореме об области значений непрерывной функции f ( x) b a a E f m, M , т.е. функция принимает все значения на отрезке m; M в том числе и число b 1 f ( x)dx . b a a E. Оценка для модуля интеграла. Если интегрируемы функции y f (x) и y f (x) на отрезке a; b , то b b f ( x)dx f ( x) dx . a a Действительно, на отрезке a; b справедливо неравенство f ( x) f ( x) f ( x) . Тогда по свойству C: b b b a a a f ( x) dx f ( x)dx f ( x) dx , откуда следует b b a a f ( x)dx f ( x) dx . 3. Интегрирование разрывных функций. h(a), x a, b ЛЕММА 3. Если функция h( x) 0, x a; b , то h( x)dx 0 . h(b), x b. a ДОК. Любая интегральная сумма S (h) , соответствующая разбиению , имеет вид h(a), 0 a h(b), n1 b S (h) h( 0 )x0 h( n1 )xn1 , где h( 0 ) и h( n1 ) . 0, 0 a 0, n1 b Тогда lim S (h) 0 . 0 ЛЕММА 4. Если функция y f (x) непрерывна на отрезке a; b , а функция y f1 ( x) b b a a определена на a; b и совпадает с f (x) на интервале a; b , то f ( x)dx f1 ( x)dx . ДОК. Функция h( x) f1 ( x) f ( x) удовлетворяет условию леммы 1 и f1 ( x) f ( x) h( x) . Тогда по свойству А следует утверждение леммы. ОПР. Функция y f (x) называется кусочно-непрерывной на отрезке a; b , если существует разбиение x0 , x1 ,..., xn отрезка a; b , для которого функция непрерывна на каждом из интервалов xk ; xk 1 и имеет разрывы первого рода в точках xk . ТЕОРЕМА 3. Всякая кусочно-непрерывная функция на отрезке a; b интегрируема. ДОК. По лемме 2 функция интегрируема на каждом отрезке xk ; xk 1 . Тогда интегрируемость функции на a; b следует из свойства B и конечности числа точек разрыва. ТЕОРЕМА 4. b Если функция y f ( x) 0 кусочно- непрерывна на отрезке a; b и f ( x)dx 0 , то a f ( x) 0 в конечном числе точек. ДОК. Если f ( ) 0 для xk ; xk 1 , то xk 1 b n x j 1 xk a j 1 x j f ( x)dx 0 и f ( x)dx f ( x)dx 0 , поскольку хотя бы одно из этих слагаемых положительно, а другие неотрицательны. Таким образом, f ( x) 0, x xk ; xk 1 ВОПРОСЫ К ЭКЗАМЕНУ. 1) Понятие интеграла Римана. Необходимое условие интегрируемости на отрезке. 2) Достаточное условие интегрируемости на отрезке (включая леммы) 3) Свойства линейности интеграла, аддитивности интеграла по множеству 4) Интегрирование неравенств. Оценка интеграла Римана. 5) Теорема о среднем для интеграла. 6) Интегрирование разрывных функций.







![Задание 7. Поиск значения обратной ... Создайте класс, содержащий метод, который для переданной на вход произвольной... [a,b]](http://s1.studylib.ru/store/data/004633031_1-8806371c9708a533a3c0570912606841-300x300.png)