Билет №1, задача №8 

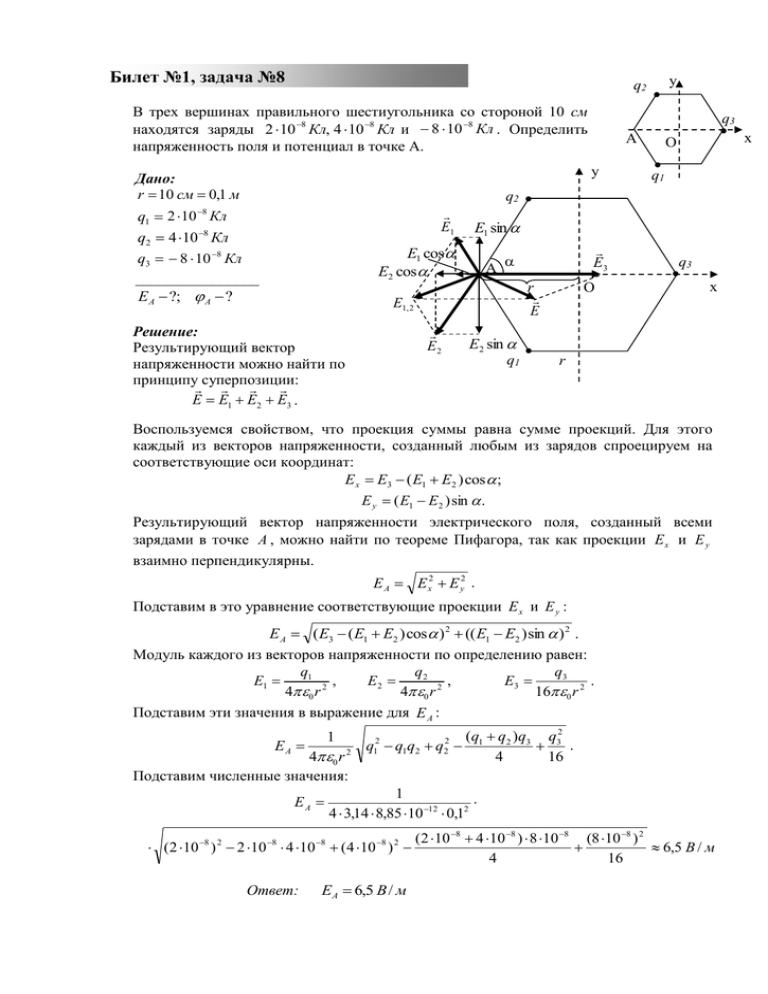
Билет №1, задача №8
q2
В трех вершинах правильного шестиугольника со стороной 10 см
находятся заряды 2  10 8 Кл, 4  10 8 Кл и  8  10 8 Кл . Определить
напряженность поля и потенциал в точке А.
A
y
Дано:
r  10 см  0,1 м

y
q3
 x
O

q1
q2 
8
q1  2 10 Кл
q2  4 10 8 Кл
q3   8  10 8 Кл
________________
E A  ?;  A  ?

E1
E1 sin 
E1 cos
E2 cos
r

E
E1, 2
Решение:
Результирующий вектор
напряженности можно найти по
принципу суперпозиции:
  

E  E1  E2  E3 .

E3
A 

E2
E2 sin  
q1
O
q3

x
r
Воспользуемся свойством, что проекция суммы равна сумме проекций. Для этого
каждый из векторов напряженности, созданный любым из зарядов спроецируем на
соответствующие оси координат:
E x  E3  ( E1  E2 ) cos  ;
E y  ( E1  E2 ) sin  .
Результирующий вектор напряженности электрического поля, созданный всеми
зарядами в точке A , можно найти по теореме Пифагора, так как проекции E x и E y
взаимно перпендикулярны.
E A  E x2  E y2 .
Подставим в это уравнение соответствующие проекции E x и E y :
E A  ( E3  ( E1  E2 ) cos ) 2  (( E1  E2 ) sin  ) 2 .
Модуль каждого из векторов напряженности по определению равен:
q3
q1
q2
E3 
E1 
E2 
,
,
.
2
2
160 r 2
40 r
40 r
Подставим эти значения в выражение для E A :
1
EA 
40 r 2
Подставим численные значения:
EA 
q12  q1q2  q22 
1

4  3,14  8,85 10 12  0,12
 (2 10 8 ) 2  2 10 8  4 10 8  (4 10 8 ) 2 
Ответ:
(q1  q2 )q3 q32
.

4
16
E A  6,5 В / м
(2 10 8  4 10 8 )  8 10 8 (8 10 8 ) 2

 6,5 В / м
4
16