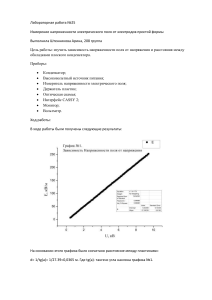
На двух проводящих концентрических сферах радиусами 0,25 м

На двух проводящих концентрических сферах радиусами 0,25 м и
0,50 м находятся заряды (–0,25) мкКл и 0,55 мкКл соответственно.
Определить модуль напряженности электрического поля на
расстоянии 0,50 м от поверхности внешней сферы.
Выполним иллюстрацию к условию задачи.
Концентрические сферы имеют общий центр,
сфера меньшего радиуса (внутренняя сфера)
заряжена отрицательным зарядом, а сфера
большего радиуса (внешняя сфера) ―
положительным.
Напряженность поля в точке М есть векторная
сумма напряженностей полей, образованных первой и второй сферами:
.
Рассчитаем модуль напряженности результирующего поля, пользуясь
алгоритмом.
1) На рисунке показаны векторы напряженности и полей,
образованных зарядами и , распределенными по поверхности внутренней
и внешней сферы соответственно. Вектор направлен к центру сфер, так
заряд является отрицательным, а вектор ― от центра сфер, так заряд является положительным.
2) Модули векторов напряженности определяются следующими
формулами:
• поля, образованного зарядом , –
| |
| |
,
где 9 ∙ 10 Н м ⁄Кл ― коэффициент пропорциональности, | | ―
модуль заряда, распределенного по поверхности внутренней сферы,
― расстояние от центра внутренней сферы до точки M, ―
радиус внешней сферы, ― расстояние от поверхности внешней сферы до
точки M;
• поля, образованного зарядом , –
,
где ― заряд, распределенный по поверхности внешней сферы, ― расстояние от центра внешней сферы до точки M.
3) Векторы напряженности направлены вдоль одной прямой в
противоположные стороны; проекции векторов напряженности на
координатную ось, направленную к центру сфер, равны:
; .
4) Проекция вектора напряженности результирующего поля:
| |
| | .
5) Модуль напряженности результирующего поля найдем по формуле
!| | !.
| | | | Произведем вычисление:
9 ∙ 10
!|0,25| 0,55! ∙ 10$% 2,7 ∙ 10' В/м 2,7кВ/м.
0,50 0,50
Таким образом, величина напряженности поля в точке М составляет
2,7 кВ/м.