Целая и дробная части числа
реклама

ÊÂÀÍT 2002/¹5
36
ÌÀÒÅÌÀÒÈ×ÅÑÊÈÉ
ÊÐÓÆÎÊ
Öåëàÿ è äðîáíàÿ ÷àñòè ÷èñëà
À.ÅÃÎÐÎÂ
Ó
ÏÎÌßÍÓÒÛÅ Â ÇÀÃËÀÂÈÈ ÔÓÍÊÖÈÈ ÄÎÂÎËÜÍÎ
÷àñòî âñòðå÷àþòñÿ â ñàìûõ ðàçíûõ îáëàñòÿõ ìàòåìàòèêè
â ÷àñòíîñòè, â àëãåáðå, àíàëèçå, òåîðèè ÷èñåë, êîìáèíàòîðèêå. Îá ýòèõ è ðîäñòâåííûõ èì ôóíêöèÿõ, à òàêæå î
çàäà÷àõ, ñ èõ ïîìîùüþ ðåøàåìûõ, ìû è ïîãîâîðèì.
Öåëàÿ ÷àñòü ÷èñëà è åå ðîäñòâåííèêè
Öåëîé ÷àñòüþ [x] ÷èñëà õ íàçûâàåòñÿ íàèáîëüøåå öåëîå
÷èñëî, íå ïðåâîñõîäÿùåå õ.
Íàïðèìåð, [1,5] = 2, [1] = 1, [0] = 0, [1,5] = 1, [ π] = 3 .
Âîîáùå, â ñèëó îïðåäåëåíèÿ, ðàâåíñòâî [x] = k îçíà÷àåò, ÷òî
k ýòî öåëîå ÷èñëî, òàêîå, ÷òî k £ x < k + 1 .
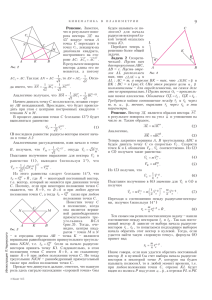
Ãðàôèê ôóíêöèè y = [x] (ðèñ.1) ñîñòîèò èç ñòóïåíåê è êàê
áû îáðàçóåò ëåñòíèöó, èäóùóþ ñëåâà íàïðàâî è ñíèçó ââåðõ,
ïåðåõîäÿùóþ â ñåáÿ ïðè
O
ïàðàëëåëüíîì ïåðåíîñå
uuur
íà âåêòîð AB = (1;1) .
 ëèòåðàòóðå òàêæå
âñòðå÷àåòñÿ òåðìèí «ïîë
÷èñëà õ» (â ïðîòèâîïî`
`
N ëîæíîñòü ñëîâó «ïîòîëîê») è åãî îáîçíà÷åíèå
`
êë xúû . Ýòî òî æå ñàìîå, ÷òî
è öåëàÿ ÷àñòü ÷èñëà.
Ñõîäíûì îáðàçîì îïÐèñ. 1
ðåäåëÿåòñÿ ôóíêöèÿ éê xùú
ïîòîëîê ÷èñëà õ. Ýòî íàèìåíüøåå öåëîå ÷èñëî, íå ìåíüøåå õ.
é 1ù
Íàïðèìåð, éê-1ùú = -1 , ê- ú = 0 , éê πùú = 4 , éê 2,5ùú = 3 .
êê 2 úú
y
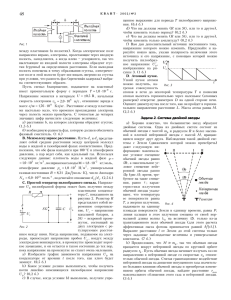
Ãðàôèê ôóíêöèè y = éê x ùú
ïîêàçàí íà ðèñóíêå 2.
Óïðàæíåíèÿ
`
`
Ðèñ. 2
é x2 - 3x ù
ú =1;
à) êê
ú
2
êë
úû
x
1. Ïîäóìàéòå, êàê èç ãðàôèêà
y = [x] ïîëó÷èòü ãðàôèê y = êé x úù ,
è âûðàçèòå éê x ùú ÷åðåç öåëóþ ÷àñòü.
2. Ðåøèòå óðàâíåíèÿ
é 3 x - 1ù
á) ê
ú=5.
êê 3 úú
Îòìåòèì íåêîòîðûå ïî÷òè î÷åâèäíûå ñâîéñòâà öåëîé ÷àñòè
÷èñëà:
1) [ x ] £ x ; 2) [ x + a ] = [ x ] + a , ãäå à ïðîèçâîëüíîå öåëîå
÷èñëî; 3) [ x + y] ³ [ x ] + [ y ] ïðè ëþáûõ õ è ó.
Óïðàæíåíèÿ
3. Äîêàæèòå, ÷òî åñëè [ x + a ] = [ x ] + [a ] äëÿ ëþáîãî x Î 4 , òî à
öåëîå ÷èñëî.
4. Ïîñòðîéòå ãðàôèêè ôóíêöèé
é xù
à) y = [2x ] ;
á) y = [-x ] ;
â) y = [ x ] - 2 ê ú .
ëê 2 ûú
5. Íàðèñóéòå íà ïëîñêîñòè õÎó òî÷êè, äëÿ êîòîðûõ
à) [ x + y] = [ x ] + [ y ] ;
6. Äîêàæèòå, ÷òî
2
2
á) éêë x + y ùúû = 1 ;
â) [ x ] = [ y] .
[ x ] + [ y ] + [ x + y ] £ [2 x ] + [2 y ] .
Íàêîíåö, èíîãäà áûâàåò ïîëåçíà ôóíêöèÿ y = (x )
áëèæàéøåå ê õ öåëîå ÷èñëî. Ïðè ýòîì åñëè áëèæàéøèõ ê õ
2k + 1
öåëûõ ÷èñåë äâà (÷òî áûâàåò ïðè x =
, ãäå k öåëîå),
2
âûáèðàåòñÿ áîëüøåå èç íèõ.
æ 1ö
Íàïðèìåð, çç- ÷÷ = 0 ,
çè 2 ø÷
æ 1 ö÷
çç ÷ = 1 , (π) = 3 , (0,8) = 1 .
çè 2 ø÷
é
1ù
Íåòðóäíî âèäåòü, ÷òî ( x) = ê x + 2 ú .
ëê
ûú
Óïðàæíåíèå 7. Äîêàæèòå ýòî è ïîñòðîéòå ãðàôèê ôóíêöèè
y = (x) .
Äðîáíàÿ ÷àñòü ÷èñëà
Äðîáíîé ÷àñòüþ {x} ÷èñëà õ íàçûâàåòñÿ ÷èñëî
{x } = x - [ x ] .
ì 1üï 1
Òàê, {-0,3} = 0,7 , ï
í- 2ý = 2 , { 2 } = 2 - 1 , {-2 2 } =
îïï þïï
= 2 - 2 , {1} = 0 .
Îòìåòèì íåêîòîðûå ñâîéñòâà äðîáíîé ÷àñòè:
1) ðàâåíñòâî {x} = x ðàâíîñèëüíî òîìó, ÷òî 0 £ x < 1 ; 2)
{x} = {y} òîãäà è òîëüêî òîãäà, êîãäà x y = n, ãäå n öåëîå
÷èñëî; â ÷àñòíîñòè, 3)
y
{x + 1} = {x} äëÿ ëþáî
ãî õ.
Òàêèì îáðàçîì, ôóíêöèÿ y = {x} ïåðèîäè÷íà
ñ ïåðèîäîì 1. Ãðàôèê åå
`
x
ïîêàçàí íà ðèñóíêå 3 (ïîêîñèâøèéñÿ ïåðèîäè÷åñÐèñ. 3
êèé çàáîð).
Ñ äðîáíîé ÷àñòüþ òåñO
íî ñâÿçàíà åùå îäíà ôóíê
öèÿ: y = {{x}} ðàññòîÿíèå îò õ äî áëèæàéøåãî
öåëîãî ÷èñëà.  îòëè÷èå îò
`
N
äðîáíîé ÷àñòè ïîñëåäíÿÿ
ôóíêöèÿ íåïðåðûâíà. Åå
ãðàôèê èçîáðàæåí íà ðèÐèñ. 4
ñóíêå 4.
Óïðàæíåíèÿ
{x + 21}- 21 .
8. Äîêàæèòå, ÷òî
{{x}} =
9. Äîêàæèòå, ÷òî
{k {x}} = {kx}
ðåøèòå óðàâíåíèå
ïðè ëþáîì íàòóðàëüíîì k, è
{3 {x }} = x .
10. Ðåøèòå óðàâíåíèÿ
1
à) {3 x } = ;
á) {6 x } + {x} = 1 .
2