6648x

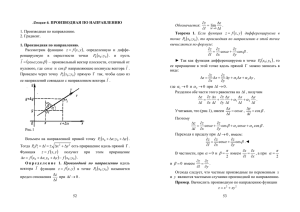
Задача 124BEB. Небольшая шайба после удара
скользит вверх по наклонной плоскости из точки A
(см. рисунок). В точке B наклонная плоскость без
излома переходит в наружную поверхность
горизонтальной трубы радиусом R. Если в точке A
скорость шайбы превосходит v0= 4 м/с, то в точке
B шайба отрывается от опоры. Длина наклонной
плоскости AB = L = 1 м, угол α = 30°.
Коэффициент трения между наклонной плоскостью
и шайбой μ = 0,2. Найдите внешний радиус трубы R.
Дано: v0= 4 м/с; AB = L = 1 м: α = 30°: μ = 0,2
Найти:R=?
Решение. В верхней точке на шайбу действует только сила тяжести (N=0 – условие
отрыва). Тогда по второму закону Ньютона для движения по окружности радиуса R:
𝑣2
𝑚 ∙ 𝑔 ∙ cos 𝛼 = 𝑚 ∙ ,
𝑅
2
𝑣 = 𝑔 ∙ 𝑅 ∙ cos 𝛼 . (1)
Если координатная ось направлена вверх, то из кинематического уравнения
2
𝑣𝑥2 − 𝑣0𝑥
= 2 ∙ 𝑎𝑥 ∙ 𝑠𝑥 ,
2
2
𝑣 − 𝑣0 = 2 ∙ 𝑎 ∙ 𝑙. (2)
По закону сохранения энергии начальная кинетическая энергия идет на увеличение
потенциальной энергии, на работу силы трения и часть ее остается:
𝑚 ∙ 𝑣02
𝑚 ∙ 𝑣2
=𝑚∙𝑔∙ℎ+
+ 𝐹тр ∙ 𝑙
2
2
𝑚 ∙ 𝑣02
𝑚 ∙ 𝑔 ∙ 𝑅 ∙ cos 𝛼
= 𝑚 ∙ 𝑔 ∙ 𝑙 ∙ sin 𝛼 +
+ 𝜇 ∙ 𝑚 ∙ 𝑔 ∙ cos 𝛼 ∙ 𝑙
2
2
𝑔 ∙ 𝑅 ∙ cos 𝛼 = 𝑣02 − 2 ∙ 𝑔 ∙ (sin 𝛼 + 𝜇 ∙ cos 𝛼) ∙ 𝑙.
Откуда
𝑣02 − 2 ∙ 𝑔 ∙ (sin 𝛼 + 𝜇 ∙ cos 𝛼) ∙ 𝑙
𝑅=
𝑔 ∙ cos 𝛼
2
𝑣0
𝑅=
− 2 ∙ 𝑙 ∙ (tan 𝛼 + 𝜇)
𝑔 ∙ cos 𝛼
Вычисления в СИ:
42
√3
𝑅=
− 2 ∙ 1 ∙ ( + 0,2) м = 0,3 м
3
√3
10 ∙ 2
Ответ.
𝒗𝟐𝟎
𝑹=
− 𝟐 ∙ 𝒍 ∙ (𝐭𝐚𝐧 𝜶 + 𝝁), 𝑹 = 𝟎, 𝟑 м.
𝒈 ∙ 𝐜𝐨𝐬 𝜶