Схема иссл функций

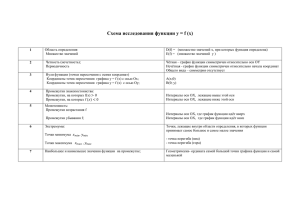
Общая схема исследования функций и построения их графиков
1о. Найти область определения функции.
Выяснить наличие вертикальных асимптот.
a) Если D(f)=R(функция выражена многочленом), то функция не имеет вертикальных
асимптот.
b) Если есть значение хо, при которой функция не существует (функция выражена
дробью), то в этих точках есть вертикальная асимптота, уравнение которой 𝑥 = 𝑥𝑜 .
Надо исследовать поведение функции вблизи этих точек. Найти пределы функции:
lim f ( x)   или lim f ( x)   .
x  x 0
xx0 0
0
2о. Выяснить наличие горизонтальных асимптот.
f ( x)
Найти предел функции: lim
х 
a) Если он равен конечному числу b, то 𝑦 = 𝑏 – горизонтальная асимптота.
b) Если он равен ∞ или не существует, то горизонтальных асимптот нет, но м.б.
наклонные.
о
3 . Выяснить наличие наклонных асимптот.
Найти пределы функции по формулам (2) и (3):
𝒌, то это есть угловой коэф. наклонной;
𝑓(𝑥)
a) lim 𝑥 = {𝟎, то накл. асимп. нет, но м. б. горизонт. ;
𝑥→∞
∞, ∄, то наклонных асимп. нет.
𝒃, то с 𝑘 уравн асимпт. 𝑦 = 𝑘𝑥 + 𝑏;
(𝑓(𝑥)
b) lim
− 𝑘𝑥) = { 𝟎, то при 𝑘 ≠ 0 урав. асимп. 𝑦 = 𝑘𝑥;
𝑥→∞
∞, ∄, то накл. и гориз. асимп. нет.
4о. Обозначить поведение функции на бесконечности,
т.е. подвести итоги пунктов 1о-b и 2о.
5о. Исследовать функцию на четность-нечетность.
Доказать равенства:𝑓(−𝑥) = 𝑓(𝑥) и 𝑓(−𝑥) = −𝑓(𝑥) и определить симметричность
графика функции.
6о. Найти нули функции и промежутки знакопостоянства:
a) точки пересечения графика с осями ох и оу при х=0 и у=0;
b) промежутки знакопостоянства при 𝑦 > 0, 𝑦 < 0.
7о. Найти экстремумы функции и промежутки монотонности.
a) 𝑦′ = 0 → найдём критические точки;
b) 𝑦 ′ > 0 → найдём промежутки возрастания функции;
c) 𝑦 ′ < 0 → найдём промежутки убывания функции;
Сделать вывод о точках экстремума.
d) Найти значение функции в точках экстремума: 𝑓(𝑥)𝑚𝑎𝑥 ; 𝑓(𝑥)𝑚𝑖𝑛 .
8о. Найти точки перегиба и промежутки выпуклости функции.
a) 𝑦 ′′ = 0 → найдём точки перегиба;
b) 𝑦 ′′ > 0 → найдём промежутки выпуклости вниз;
c) 𝑦 ′′ < 0 → найдём промежутки выпуклости вверх;
d) Найти значение функции в точках перегиба.
9о. Завершить построение графика функции, найдя дополнительные точки,
уточняющие его вид.
Заметим, что исследование функции проводится одновременно с построением её
графика.