Репетиционное тестирование, 2

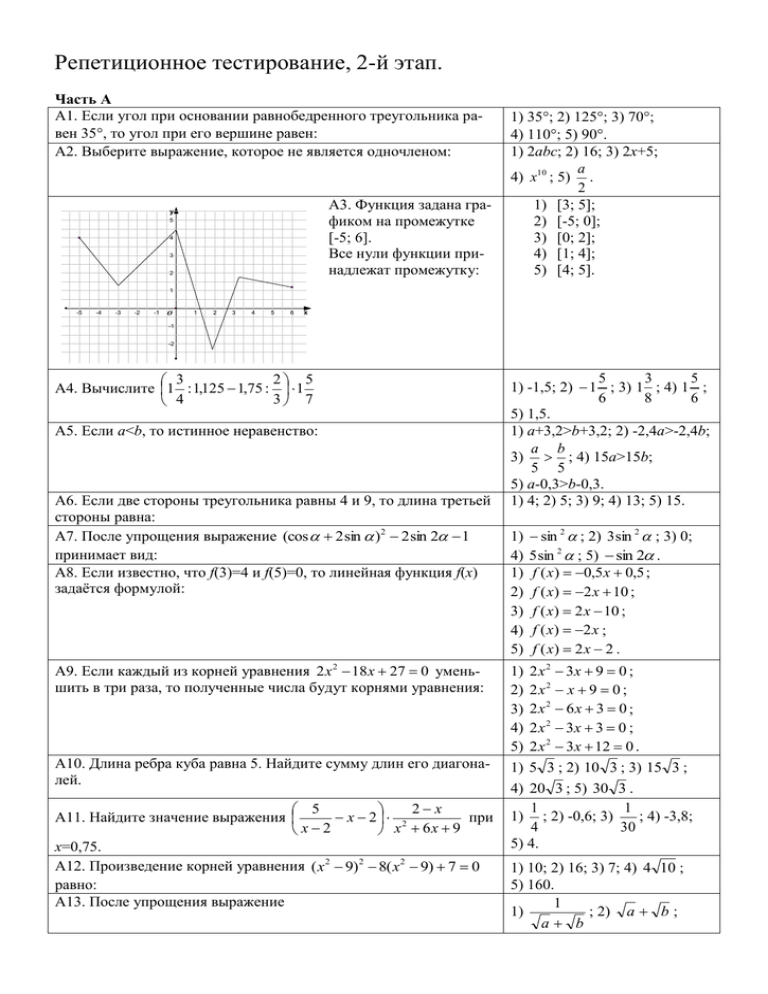
Репетиционное тестирование, 2-й этап.
Часть А
А1. Если угол при основании равнобедренного треугольника равен 35, то угол при его вершине равен:
А2. Выберите выражение, которое не является одночленом:
A3. Функция задана графиком на промежутке
[-5; 6].
Все нули функции принадлежат промежутку:
y
5
4
3
2
1) 35; 2) 125; 3) 70;
4) 110; 5) 90.
1) 2abc; 2) 16; 3) 2x+5;
a
4) x10 ; 5) .
2
1) [3; 5];
2) [-5; 0];
3) [0; 2];
4) [1; 4];
5) [4; 5].
1
-5
-4
-3
-2
-1
O
1
2
3
4
5
6
x
-1
-2
2 5
 3
А4. Вычислите 1 : 1,125  1,75 :   1
3 7
 4
А5. Если a<b, то истинное неравенство:
A6. Если две стороны треугольника равны 4 и 9, то длина третьей
стороны равна:
А7. После упрощения выражение (cos   2 sin  )2  2 sin 2  1
принимает вид:
А8. Если известно, что f(3)=4 и f(5)=0, то линейная функция f(x)
задаётся формулой:
А9. Если каждый из корней уравнения 2 x 2  18 x  27  0 уменьшить в три раза, то полученные числа будут корнями уравнения:
А10. Длина ребра куба равна 5. Найдите сумму длин его диагоналей.
2 x
 5

 x  2  2
А11. Найдите значение выражения 
при
x2
 x  6x  9
х=0,75.
А12. Произведение корней уравнения ( x 2  9)2  8( x 2  9)  7  0
равно:
А13. После упрощения выражение
5
3
5
1) -1,5; 2)  1 ; 3) 1 ; 4) 1 ;
6
8
6
5) 1,5.
1) а+3,2>b+3,2; 2) -2,4a>-2,4b;
a b
3)  ; 4) 15a>15b;
5 5
5) a-0,3>b-0,3.
1) 4; 2) 5; 3) 9; 4) 13; 5) 15.
1)
4)
1)
2)
3)
4)
5)
 sin 2  ; 2) 3 sin 2  ; 3) 0;
5 sin 2  ; 5)  sin 2 .
f ( x)  0,5 x  0,5 ;
f ( x)  2 x  10 ;
f ( x)  2 x  10 ;
f ( x)  2 x ;
f ( x)  2 x  2 .
1)
2)
3)
4)
5)
1)
4)
2 x 2  3x  9  0 ;
2x2  x  9  0 ;
2x2  6x  3  0 ;
2 x 2  3x  3  0 ;
2 x 2  3x  12  0 .
5 3 ; 2) 10 3 ; 3) 15 3 ;
20 3 ; 5) 30 3 .
1
1
1) ; 2) -0,6; 3)
; 4) -3,8;
4
30
5) 4.
1) 10; 2) 16; 3) 7; 4) 4 10 ;
5) 160.
1
1)
; 2) a  b ;
a b

a
b
2 ab  
ab  b 

 

 a  b  a  b  a  b    a  a  b  принимает вид:

 

А14. Одна сенокосилка скашивает поле за 6 часов, а вторая – за 5
часов. За какое время, работая вместе, обе сенокосилки скосят
88% этого поля?
( x 2  7)( x  7) 2
А15. Количество целых решений неравенства
0
35  x 2
равно:
А16. Среди приведенных величин положительной является:
А17. Если радиус окружности, вписанной в прямоугольный треугольник, равен 2, а гипотенуза равна 11, то площадь треугольника равна:
А18. Из данных функций выберите чётную:
3) a  b ; 4) a  b ; 5)
a  b.
1) 2,2 ч; 2) 2,6 ч; 3) 2,8 ч;
4) 3,2 ч; 5) 2,4 ч.
1) 15; 2) 8; 3) 14; 4) 12; 5) 11.
1) tg5; 2) cos10; 3) sin4;
4) sin7; 5) ctg2.
1) 22; 2) 44; 3) 26; 4) 30; 5) 52.
2
2
 x 2 ; 2) y  ;
x
x
|x|
2
 1 ; 4) y 
3) y 
 x2 ;
x
| x|
5) y  x | x | .
1) y 
Часть В
В1. Если в правильной 4-угольной пирамиде боковое ребро равно 6, а площадь диагонального сечения 12 2 , то площадь поверхности пирамиды равна…
 x 2  2 xy  y 2  xy  5,
В2. Решите систему уравнений 
Найдите наименьшее значение х+у, где
 x  y  3.
(х; у) – решение системы.
В3. Найдите сумму первых двадцати членов арифметической прогрессии ( an ) , если
a3  a5  a8  a13  a16  a18  33 .
В4. Решите уравнение x 2  3x  4  2 x  3x  4  0 . В ответ запишите произведение корней (корень, если он один).
В5. Среднее арифметическое всех целых значений функции f ( x)  53  22 sin 6 x равно…
В6. Найдите произведение большего корня на количество корней уравнения | x3  2 x 2  4 | x3  4 .
В7. Внутри угла величиной 60 размещена точка, которая находится на расстоянии 7 и 2 7 от
сторон угла. Найдите расстояние d от этой точки до вершины угла. В ответ запишите d  3 .
В8. Сумма корней уравнения 3  sin x  2  cos x , которые принадлежат промежутку [-1; 4],
равна…
В9. Диагонали AC и BD трапеции ABCD (AD || BC) пересекаются в точке О. Найдите площадь трапеции, если известно, что OD:BO=3, а площадь треугольника OCD равна 9.
( x 2  9 x  10) 2 36( x  2) 2
В10. Найдите произведение корней уравнения x 2  3x  2 
.
 2
x 2  3x  2
x  3x  2
В11. В прямоугольном треугольнике АВС с вершины А прямого угла проведены медиана AD, биссектриса АК и высота АН. Найдите гипотенузу с этого треугольника, если известно, что DK=3 и
KH=2. В ответ напишите c  5 .
В12. Три автомобиля двигаются по дороге в одну сторону с постоянными скоростями. Когда первые два из них находились в одном пункте, третий отставал от них на 30 км. Когда третий автомобиль догнал второй, первый отставал от них на 6 км. Найдите расстояние (в км) между первым и
вторым автомобилем в тот момент, когда первый и третий находились в одном пункте.