МОУ гимназия №1 г. Липецка планирование составлено на основе авторского планирования

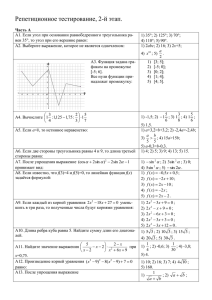
МОУ гимназия №1 г. Липецка
Предмет – геометрия
Класс – 9Б
Учитель Попова Ольга Николаевна
Программно-методическое обеспечение:

планирование составлено на основе авторского планирования
Л. С. Атанасяна, В. Ф. Бутузова, Ю. А. Глазкова по учебнику «Геометрия 7 –
9» 7 класс;

Учебник «Геометрия 7 – 9 » 7 класс Л.С. Атанасян и др., М.:
Просвещение, 2007.
Тема урока: «Площадь треугольника».
Тип урока: урок изучения нового материала
Цели урока:
образовательные: изучить и доказать теорему о площади треугольника и
рассмотреть применение теоремы при решении задач на нахождение
площадей
треугольников
и
четырехугольников,
совершенствовать
вычислительные навыки;
развивающие: развивать умения наблюдать, сравнивать, анализировать,
переходить к обобщению наблюдаемых фактов, проводить доказательство
геометрических предложений, использовать установленные ранее факты для
обоснования новых фактов и для решения конкретных задач, расширять
математический и общий кругозор, совершенствовать графическую культуру
и устную математическую речь;
воспитательные: формировать такие качества личности как познавательная
активность,
любознательность,
внимательность,
критичность,
организованность, самостоятельность, умение слушать мнение других.
Оборудование: задания для работы по готовым чертежам, раздаточный
материал для самостоятельной работы на 2 варианта (тест).
Ход урока
1. Организационный этап:
-приветствие;
-проверка готовности учащихся к уроку: наличие чертежных инструментов,
тетрадей, учебников.
Учитель. На сегодняшнем уроке (тема пока не называется: «Площадь
треугольника») докажем одну из важнейших теорем о площади. Эта теорема
используется для определения площадей различных фигур. Для
доказательства теоремы потребуются знания по теме: «Синус, косинус и
тангенс угла. Координаты точки. Площадь треугольника».
Попробуем применить новые знания для подготовки к ГИА и ЭГЕ по
математике.
2. Актуализация знаний
Повторение и проверка знаний по теме: «Синус, косинус и тангенс угла.
Площадь треугольника».
Математический диктант
1.Дать определение
тригонометрических функций
острого угла
прямоугольного треугольника.
2. Записать значения тригонометрических функций различных углов. Углы
называются произвольным образом. Работа выполняется на листочках и по
окончании осуществляется взаимопроверка. Таблица значений приводится
на экране или на доске. По результатам опроса можно предложить
дополнительный способ запоминания значений тригонометрических
функций с помощью ладони (можно в конце урока).
3.Как найти синус и косинус тупого угла? Ответ озвучивается и записывается
на доске (по формулам приведения).
300 450 600
sin 
cos 
tg
1
2
2
2
3
2
3
2
2
2
1
2
3
3
1
3
sin( 1800   )
=
sin 
Синус тупого угла равен синусу смежного с ним острого угла.
cos(1800   ) =  cos 
Косинус тупого угла равен «–» косинусу смежного с ним острого угла.
Повторение по теме: «Площадь треугольника»
1. Назовите известные формулы для нахождения площади треугольника.
К
S = 12 a b
S
6
В
3
A
14
D
1
6 3
2
S 9
S = 12 a b
В
S
1
AK  AB
2
S
S = 12 a ha
К
S
6
5
4
В
Формула
Герона
S = p(p – a)(p – b)(p – c)
р - полупериметр
Египетский
треугольник
С
S 6
3
A
В
1
СА  СB
2
1
S   4 3
2
1
14  6
2
S  42
A
Повторение
S
1
ВK  AD
2
5
6 6
6
A
7
С
S  9(9  5)(9  6)(9  7)  9  4  3  2  3 2 6
2.Устная работа по готовым чертежам на применение формул площади
прямоугольного и произвольного треугольника.
3. Египетский треугольник и его площадь.
4.Формула Герона.
Из истории математики
Сообщение подготовлено учеником. Портреты ученых предъявляются с
экрана или в бумажном варианте.
Формула для вычисления площади треугольника по трём его сторонам была
открыта Архимедом (III в. до н. э.). Однако соответствующая работа
Архимеда до наших дней не дошла.
Эта формула содержится в «Метрике» Герона Александрийского (I в. н. э.) и
названа в его честь. Герон интересовался треугольниками с целочисленными
сторонами, площади которых также являются целыми. Такие треугольники
носят название героновых треугольников. Простейшим героновым
треугольником является египетский треугольник.
Составление опорного конспекта по теме: «Площадь треугольника»
(начало)
Формулы для вычисления
площади треугольника
h
a
S = 12 a ha
b
S = 12 a b
a
c
b
a
S = p(p – a)(p – b)(p – c)
3. Изучение нового материала.
Учитель. Предлагает учащимся самостоятельно назвать тему урока и
записать в тетрадь дату и тему: «Площадь треугольника».
Обучающиеся обосновывают актуальность темы тем, что многоугольники
можно разделить на треугольники и найти площади различных
многоугольников, используя формулу площади треугольника.
Доказательство теоремы
1.Площадь треугольника равна половине произведения двух его сторон на
синус угла между ними (формулировка).
2.Условие
Дано: ∆ АВС, ВС = а, СА = b, S – площадь треугольника.
3.Заключение
1
Доказать: S  absin 
2
Теорема о площади треугольника
sin  
y
y = a sina
B
S = 12 b hb
a
y
S

C
y
a
x
b
H
A
1
AC  BH
2
1
S  b  (a  sin  )
2
S = 12 a b sina
Доказательство основано на введении системы координат и расположении
в ней определенным образом заданного треугольника.
Работа по учебнику
п.96 с.256. Рассмотреть доказательство и определить, на чем оно
основано (на использовании координат точки).
4.Первичное закрепление по готовым чертежам с самопроверкой.
1.Записать выражение для нахождения площади треугольника с
использованием трех различных углов.
2.Найти площади предложенных треугольников.
B
Найти площадь треугольника
1
S   AB  BC  sin B
2
1
S   AС  BА  sin А
2
S = 12 a b sina
B
S
4
1
S   AС  BС  sin С
2
450
C
Найти B
1
2
S = a b sina
2
6
?
A
C
S = 2 3 см2
B
300
S 2
A
2
Найти BC
S = 3 см2
2
2
S  2 2 
A
C
1
 4  2  sin 450
2
S = 12 a b sina
B
1
2 3   2  4  sin 
2
600
1
3   2  b  sin 300
2
3  b
1
2
2
b6
4
2
2 3  4  sin  :4
A
C
sin  
B
4
C
120
1200
2
A
3
2
0
 1 600  2 120
Динамическая пауза. Комплекс упражнений зарядки для глаз.
5.Работа по учебнику
Решение задачи №1021( на доказательство)
№ 1021 Докажите, что площадь параллелограмма
равна произведению двух его смежных на
синус угла между ними.
S ABD 
S = 12 a b sina
B
C
 ABD   CBD
S ABD  SCBD
a
A
1
ab sin 
2
S ABCD  2  S ABD

b
D
S ABCD  2 
1
ab sin 
2
S = a b sina
6.Составление опорного конспекта (продолжение)
Формулы для вычисления
площади треугольника
h
a
S = 12 a ha
B
a
S = 12 a b sina

C
A
b
B
параллелограмм
C
S = a b sina
a
b
1
2
a
S = ab
c
b
a

A
D
b
A 
a
B
ромб
C
a
S = p(p – a)(p – b)(p – c)
S = a2 sina
D
7.Самостоятельная работа обучающего характера по вариантам
(сделать заготовку на переносной доске)
Работа выполняется в тетрадях. Два ученика работают у доски.
ВАРИАНТ 1
B
C
ВАРИАНТ 2
АВСD – параллелограмм,
АВ = 6, AD = 4.
Найти SABCD
6
450
A
A
4
S = a2 sina
4
4
S = a b sina
600
Найти SABCD
B
C
D
S  4 2  sin 450
S  16 
S ABCD  4  6  sin 60 0  4  6 
3
 12 3
2
D
S 8 2
2
2
8.Подготовка к ГИА и ЕГЭ по математике
Задание В3
Базовые задачи (разбираются и решаются устно)
№1
В равнобедренном треугольнике ABC с основанием AC
боковая сторона AB равна 10, а высота, проведенная к
основанию, равна
. Найдите косинус угла
На клетчатой бумаге с клетками размером 1 см
1 см изображен треугольник (см. рисунок).
Найдите его площадь в квадратных
сантиметрах.
10
№2
Найти площадь параллелограмма, если одна из его сторон равна 7, другая
равна 10, а один из углов равен 30 градусам.
№3
Найти площадь ромба, если его стороны равны 11 , а один из углов равен 150
градусам.
Ответы: 0, 5 и 12;
35; 5,5
9. Тест по материалам, рекомендованным для подготовки к ГИА
Выполняется на листочках, сдается на проверку и оценивается.
Учащимся предлагается записать ответы в тетрадь и провести самопроверку.
Ответы озвучиваются учителем.
Ответы к тестам:
Вариант 1: №1 6;
№2 15;
Вариант 2: №1 49;
№2 2 3 ;
4
;
5
№3 18;
№3
№4 г.
№4 а.
ВАРИАНТ 1
1. Используя данные, указанные на
рисунке, найдите катет МК.
Р
М
ВАРИАНТ 2
1. Используя данные, указанные на
рисунке, найдите площадь
параллелограмма.
150º
6 2
7
45º
14
К
2. Найдите площадь ромба ONMK,
2. Найдите площадь
параллелограмма, стороны которого если его сторона равна 2, а М=120º.
равны 2 3 и 5, а один из углов равен
120º.
3. Используя данные, указанные на
рисунке, найдите синус угла P.
3. Используя данные, указанные на
рисунке, найдите катет BD.
C
К
5
4
Р
3
36
М
60º
B
4. Угол при основании
равнобедренного треугольника равен
30º, а площадь треугольника равна
9 3 см2. Найдите боковую сторону
треугольника.
а) 6 3 см;
в) 4 3 см;
б) 4 6 см;
г) 6 см.
D
4. Угол при вершине
равнобедренного треугольника равен
120º, а основание равно 14 3 см.
Найдите площадь треугольника.
а) 49 3 см2;
в) 42 см2;
б) 36 3 см2;
г) 48 см2.
10. Домашняя работа:
п.96, опорный конспект, №1022, №1023.
11.Подведение итогов урока. Рефлексия
Выставление отметок за работу на уроке.
Подведение итогов урока.
12.Резервное задание
Выполняется самостоятельно, с последующей проверкой.
В
5
150
Найдите площадь
равнобедренного треугольника
с углом при основании 150
5
и боковой стороной,
равной 5 см.
150
A
С
S = 12 a b sina
S
1
25
25 1 25
 5  5  sin 150 
 sin 30   

2
2
2 2 4
1
 6 (см 2 )
4