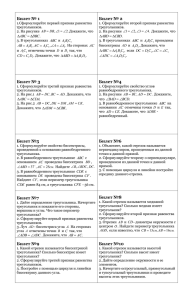
в) область значений функции.

10 класс. Математика.
Повторение.
1. Обобщение и систематизация знаний о функциях.
Как сказал известный математик Е. Вигнер, вся глубина мысли, заложенной в формулировании
математических понятий, впоследствии раскрывается тем умением, с которым это понятие
используется. С помощью
одной и той же функции
люди
получили
уникальную возможность
исследовать
самые
различные
по
своей
природе
процессы.
Казалось бы, что общего
между увеличением потока
информации
и
уменьшением атмосферного давления при возрастании высоты над уровнем моря? Между
размножением бактерий в определенной среде и количеством древесины, которое со временем
увеличивается на дереве?
Да, все эти явления можно описать и изучить с помощью одной и той же функции. Сегодня мы
повторим то, без чего невозможно дальнейшее продвижение вперед — все, что вы выучили о
функции.
Пользуясь рис. 1, учащиеся отвечают на следующие вопросы.
1. Какова область определения данной функции?
2. Найдите область значений функции f ( x ) .
3. Определите по графику нули функции и промежутки ее знакопостоянства.
4. Назовите промежутки возрастания и убывания функции.
5. Является данная функция четной или нечетной?
6. Каковы наибольшее и наименьшее значения данной функции? При каких значениях аргумента
функция принимает свое наибольшее (наименьшее) значение?
1. Дайте определение функции.
2. Что называют областью определения; областью значений функции?
3. Что такое график функции?
4. Как можно задать функцию?
5. В каком случае линии, изображенные на рис. 2, а—г, являются графиком функции? Ответ
обоснуйте.
6. Что называют нулями функции? Как найти нули функции?
7. Какие функции называются нечетными; четными?
8. Дайте определение функции, возрастающей (убывающей)
на множестве М.
Решение упражнений
1
1. Функция задана формулой f(x) = 2 𝑥 2 + 3𝑥. Найдите:
а) f(2) и f(-1);
б) нули функции.
2. Найдите область определения функции:
𝒙𝟐 +4
9
а) f ( x ) = 𝑥 𝟐 −10𝑥+24 ; б ) у = √7𝑥 − 𝑥 2 ;
в ) у = √15−2𝑥−𝑥 2
3 . Постройте график функции f(x) = 𝑥 2 + 2𝑥 − 3. Пользуясь графиком найдите:
а) промежутки, при которых f(x) > 0 и на которых f(x) < 0 ;
б) промежутки возрастания функции;
в) область значений функции.
2. Обобщение и систематизация системы опорных фактов курса планиметрии.
Основные подходы к изучению стереометрии и решению задач похожи на те, что используются в
планиметрии. Вспомним, как построен курс планиметрии (основные фигуры, аксиомы, теоремы,
опорные факты)
1. Сформулируйте свойства равнобедренного треугольника.
2. Сформулируйте признаки равнобедренного треугольника.
3. Сформулируйте три признаки равенства треугольников.
4. Назовите известные вам соотношения между сторонами и углами треугольника,
прямоугольного треугольника.
5. Сформулируйте теорему Пифагора, теорему синусов; теорему косинусов.
6. Сформулируйте признаки равенства треугольников.
7. Запишите формулы площади треугольников. Какие свойства средней линии
треугольника?
8. Какая геометрическая фигура называется четырехугольником?
9. Чему равна сумма внутренних углов четырехугольника; внешних?
10. Какие виды четырехугольников вам известны?
11. Сформулируйте свойства и признаки параллелограмма, ромба, прямоугольника,
квадрата.
12. Что называют трапецией? Какие виды трапеции вам известные?
13. Сформулируйте свойства равнобедренной трапеции.
14. Назовите формулы для определения площади известных вам видов
четырехугольников.
15. Какой четырехугольник называется вписанным в окружность? описанным
около окружности?
16. Сформулируйте свойство углов вписанного четырехугольника?
17. Какое свойство имеют стороны описанного четырехугольника?
Задачи по готовым чертежам.
2. По данным рисунка 1 докажите, что ΔАВС равнобедренный.
3. По данным рисунка 2 найдите КВ.
4. По данным рисунка 3 найдите а, в, h.
5. На рисунке 4 АВСД – прямоугольник; ОК=4. Найдите АС.
4
Письменные задания
1. Найдите площадь треугольника со сторонами 7см, 15см и 20см.
2. Найдите площадь трапеции, если её диагонали равны 2√3см и 3√2, а угол между ними
составляет 45º.
3. Найдите площадь прямоугольника, диагональ которого 13см, если разность двух соседних
сторон равна 7см.
Решения принимаются до 8 сентября 2014 года на электронную почту,
размещённую на странице «Контакты»