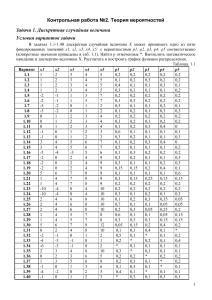
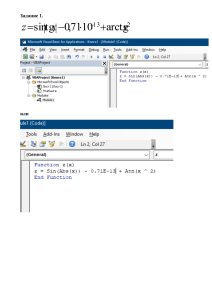
1.9. Телефонный номер состоит из шести цифр, каждая из которых равновозможно принимает
значения от 0 до 9. Найти вероятность того, что все цифры одинаковы.
1.11. Условие задачи 1.9. Вычислить вероятность того, что номер не содержит цифры пять.
Решение.
Обозначим событие А- событие состоящее в том, что номер не содержит цифры 5.
Для нахождения вероятности события А воспользуемся классическим определением вероятности
Р(A)=
m
n
Где n 106 – общее число всевозможных номеров (число перестановок с повторениями 10 цифр по 6
местам)
m=95=59049 – число номеров в которых нет пятерки (число перестановок с повторениями 9 цифр по 5
местам)
тогда
Р(A)=59049/1000000=0,0590
Ответ: Р(A)=0,0590
В задачах 2.1-2.40 приведены схемы соединения элементов, образующих цепь с одним входом и
одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности
событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где
находится данный элемент. Вероятности отказа элементов 1, 2, 3, 4, 5 соответственно равны p1=0,1; p2=0,2;
p3=0,3; p4=0,4; p5=0,5. Найти вероятность того, что сигнал пройдет со входа на выход.
№2,11
р1=0,1 р2=0,2 р3=0,3 р4=0,4
Обозначим Аi – событие состоящее в том, что i-ый элемент работает. В – событие состоящее в том, что
сигнал пройдет через цепь.
В=А1А2А3А4
Так как события Аi независимы, то
Р(В)=Р(А1)р(А2) р(А3) р(А4)=(1-р1)(1-р2)(1-р3)(1-р4)
Р(В)=(1-0,1)(1-0,2)(1-0,3)(1-0,4)=0,9*0,8*0,7*0,6=0,3024,
Ответ: Р(В)=0,3024
3.11. Группа студентов состоит из пяти отличников, десяти хорошо успевающих и семи
занимающихся слабо. Отличники на предстоящем экзамене могут получить только отличные оценки.
Хорошо успевающие студенты могут получить с равной вероятностью хорошие и отличные оценки.
Слабо занимающиеся могут получить с равной вероятностью хорошие, удовлетворительные и
неудовлетворительные оценки. Для сдачи экзамена вызывается наугад один студент. Найти вероятность
того, что студент получит хорошую или отличную оценку.
Решение.
Обозначим А – событие состоящее в том, что в студент получит хорошую или отличную оценку
Можно выдвинуть три гипотезы
Н1– вызвали отличника
Р(Н1)=5/22
Н2– вызвали хорошо успевающих
Р(Н2)=10/22
Н3– вызвали слабо успевающих
Р(Н3)=7/22
Условная вероятность того, что отличник сдаст на хорошо или отлично
РН1(А)=1
Хорошо успевающий
РН2(А)=1
Слабо успевающий
РН3(А)=1/3
Вероятность события А найдем по формуле полной вероятности
Р(А)= Р(Н1)* РН1(А)+ Р(Н2)* РН2(А)+ Р(Н3)* РН3(А)
Р(А)=5/22*1+10/22*1+7/22*(1/3)=
15 30 7 52 26
66
66 33
Ответ: Р(А)=26/33
4.11. Монету подбрасывают восемь раз. Чему равно наивероятнейшее число выпадений герба?
Решение.
р=0,5-вероятность выпадения герба при одном броске, n=8- число бросков
Наивероятнейшее число стандартных деталей найдем по формуле
np-q≤k<np+p
0,5*8-0,5≤k<8*0,5+0,5
3,5≤k<4,5
k=4
Ответ: к=4
ЗАДАЧА 5
В задачах 5.1-5.30 дискретная случайная величина Х может принимать одно из пяти фиксированных
значений x1, x2, x3, x4, x5 с вероятностями p1, p2, p3, p4, p5 соответственно (конкретные значения
приведены в табл. 1.1). Вычислить математическое ожидание и дисперсию величины Х. Рассчитать и
построить график функции распределения.
№5,11
Х
0
1
2
3
4
Р
0,1
0,2
0,3
0,4
0
Математическое ожидание
n
М(Х)=
X р
i 1
i
i
М(Х)= 0*0,1+1*0,2+2*0,3+3*0,4+4*0=2,0
Дисперсия
Д(Х)=М(Х2)–( М(Х))2
n
Где М(Х2)=
X
i 1
2
i
рi
М(Х2)= 02*0,1+12*0,2+22*0,3+32*0,4+42*0=5
Д(Х)=5–22=1
Функция распределения
F(xi)=P{X<xi}=P{(X=x1)(X=x2) ... (X=xi-1)}= p1+...+pi-1.
0, x 0
0.1, 0 x 1
F(X)= 0.3,1 x 2
0.6, 2 x 3
1,3 x
График функции распределения
ЗАДАЧА 6
В задачах 6.1-6.30 (параметры заданий приведены в табл. 1.2) случайная величина Х задана
плотностью вероятности
Определить константу С, математическое ожидание, дисперсию, функцию распределения величины Х,
а также вероятность ее попадания в интервал [α, β].
№6.11
0, x 0иx 4
f(x)=
c cos(2 x), 0 x
4
Для определения постоянной с воспользуемся свойством плотности вероятности
f ( x)dx 1
c4
c
c
c
c
c
cos(2
x
)
dx
cos(2 x)d (2 x) sin(2 x) 4 (sin sin 0) (1 0)
0
20
2
2
2
2
2
0
4
с/2=1
с=2
0, x 0иx 4
f(x)=
2 cos(2 x), 0 x
4
математическое ожидание
М(Х)=
xf ( x)dx
М(Х)=
ux
du dx
x
14
1
2
2
x
cos(2
x
)
dx
2(
sin(2
x
)
sin(2 x)dx) 2( 0 cos(2 x) 4 )
0.2854
4
dv cos(2 x)dx
0
2
20
8
4
4
0
0
1
v sin(2 x)
2
4
Дисперсия
Д(Х)=М(Х2)–(М(Х))2
2
Где М(Х )=
x
2
f ( x)dx
u x2
du 2 xdx
4
M ( X 2 ) 2 x 2 cos(2 x)dx dv cos(2 x)dx 2(
0
1
v sin(2 x)
2
4
x
sin(2 x) 4 x sin(2 x) dx) 2( x sin(2 x) dx)
2
32 0
0 0
2
4
2
ux
du dx
x
14
2
1
dv sin(2 x)dx 2( ( cos(2 x) 4 cos(2 x)dx)) 2( (0 0 sin(2 x) 4 ))
32
2
20
32
4
0
0
1
v cos(2 x)
2
2
1
2 8
2( (1 0))
0.1169
32 4
16
2
Д(Х)=0,1169–0,28542 =0.0354
Функция распределения
x
F(x)=
f ( x)dx
x
F(X)=
0dx 0 при x<0
x
F(X)= 2 cos(2 x)dx sin(2 x)
0
4
F(X)=
x
0
sin(2 x) при 0≤x≤
2 cos(2 x)dx sin(2 x) 4 1 при
0
0
<x
4
4
=
0, x 0
F(X)= sin(2 x ), 0 x
4
1, x 4
1
0.5
F( x)
10
5
0
5
10
0.5
1
x
Вероятность того, что 0,5<x<1 найдем по формуле
1
Р(0,5<x<1)=
0.5
2sin(2 x)
f ( x)dx 2 cos(2 x)dx
4 (sin( ) sin(1)) 1 0.8415 0.1585
2
2
0.5
0.5
4
ЗАДАЧА 7
В задачах 7.1-7.30 (условия приведены в табл. 1.3) случайная величина Х распределена равномерно
на интервале [a,b]. Построить график случайной величины Y=ϕ(X) и определить плотность вероятности
g(y).
№7.11
Y=2х
Плотность вероятности СВ Х найдем по формуле
f(x)=
1
, x [ a; b ]
ba
f(x)=1/(6+4)=0.1
График функции Y=2х при -4≤x≤6
20
10
f( x)
0
10
0
5
x
x=0.5y
х’=(0.5y)’=0.5
g(y)=f(0.5y)*(0.5)=0.1*0.5=0.05
свойство плотности вероятности
g ( y)dy 1
12
0, 05dy 0, 05 y
8
12
8
0.05 12 8 1
0, y 8
Ответ: g(y)= 0.05, 8 y 12
0, y 12
ЗАДАЧА 8.
В задачах 8.1-8.30 (конкретные параметры приведены в табл. 1.4) двухмерный случайный вектор
(Х, У) равномерно распределен внутри выделенной жирными прямыми линиями на рис. 1.1 области B.
Двухмерная плотность вероятности f(x,y) одинакова для любой точки этой области B:
Вычислить коэффициент корреляции между величинами X и Y.
№8.11
y=x
y=4-x
Коэффициент корреляции
r=
K xy
X y
плотность распределения СВ (x,y) найдем по формуле
f(x,y)=1/S
где S–площадь фигуры
S=0.5*2*4=4
f(x,y)=1/4
Плотность распределения f(x) найдем по формуле
f(x)=
f ( x, y )dy
x
f(x)=
1
1 x x
dy
y , 0<x≤2
0 4
4 0 4
1
1 4 x 4 x
dy y
, 2<x≤4
4
4 0
4
4 x
f(x)=
0
0, x 0
x
,0 x 2
4
f(x)=
4 x ,2 x 4
4
0, x 4
f(y)=
f ( x, y )dx
4 y
f(y)=
y
1
1 4 y 1
2 y
,0<y≤2
dx x
(4 y y )
4
4 y
4
2
0, y 0
2 y
f(y)=
,0 y 2
2
0, y 2
Математическое ожидание
М(Х)=
xf ( x)dx
М(Y)=
yf ( y)dy
4
x2
4x x2
x3 2 1
x3 4 8 1
64
8
2 96 64 24 8 2 4
2
M ( X ) dx
dx
(2 x ) (32
(8 ))
2
4
12 0 4
3 2 12 4
3
3
3
12
3 3
0 4
2
2
2
М(Y)= 0.5(2 y y 2 )dy 0.5( y 2
0
y3 2
12 8
2
) 0.5(
)
3 0
3
3
( x M ( x))( y M ( y)) f ( x, y)dxdy
К=
2 4 y
k
0
y
4 y
2 1
1
2 x2
1
2 (4 y) 2
y2
( x 2)( y ) dxdy ( y )( 2 x)
dy ( y )(
2(4 y)
2 y)dy
y
3 4
40
3 2
40
3
2
2
2
2
0
Среднее квадратическое отклонение
X M ( X 2 ) ( M ( X )) 2
Y M (Y 2 ) ( M (Y )) 2
2
M (X 2)
0
4
x3
4 x 2 x3
x 4 2 1 4 x3 x 4 4 16 0 1 256 256 32 16
176 14
dx
dx
(
)
(
( )) 1
4
4
16 0 4 3
4 2
16
4 3
4
3 4
48
3
2
14
2
(2)2
3
3
X
2
М(Y2)=
2
3
0.5(2 y y )dy 0.5(
0
2 2 2
2
( )
3 3
3
Y
r=
2 y3 y 4 2
64 48
2
) 0.5(
)
3
4 0
12
3
0
2
2
3
3
0
r=0
Ответ: r=0
ЗАДАЧА 9.
В задачах 9.1-9.30 вычислить математическое ожидание и дисперсию величин U и V, а так же
определить их коэффициент корреляции RUV:
U = a0 +a1X1 +a2X2
V = b0 + b1X2 + b2X3 .
Конкретные значения коэффициентов ai, i = 0, ..., 2; bj, j = 0, ..., 2 и числовые характеристики
случайных величин Xi, i = 0, ..., 3 приведены в табл. 1.9.
№9,11
Решение:
U 1 7 X1 X 2
V 7 5 X 2 5 X 3
m1 0
m2 3
m3 1
D1 4
D2 25
D3 9
K12 5
K 23 7.5
K13 3
Коэффициент корреляции найдем по формуле
rVU
M (VU ) M (V ) M (U )
V2 U2
Воспользуемся свойством математического ожидания
M (V ) M (7 5 X 2 5 X 3 ) 7 5m2 5m3 7 5 3 5 1 27
M (U ) M (1 7 X1 X 2 ) 1 7m1 m2 1 7 0 1 3 2
Дисперсия
D(U ) D(1 7 X1 X 2 ) 49D1 1D2 2 1 7 K12 49 4 1 25 14 5 151
D(V ) D(7 5 X 2 5 X 3 ) 25D2 25D3 2 (5) (5) K23 25 25 25 9 50 7.5 1225
M (VU ) M (7 5 X 2 5 X 3 )(1 7 X 1 X 2 ) M (7 2 X 2 5 X 3 49 X 1 35 X 1 X 2 35 X 1 X 3
5 X 22 5 X 2 X 3 ) 7 2m2 5m3 49m1 35 K12 m1m2 35 K13 m1m3 5 D2 m22
5 K 23 m3m2 7 2 3 5 1 49(5 (0) 3) 35(3 0 1) 5(25 32 )
5(7.5 3 1) 63.5
Коэффициент корреляции
rVW
63.5 27 (2)
0.2732
1511225
2. КОНТРОЛЬНЫЕ ЗАДАЧИ ТИПОВОГО РАСЧЕТА ПО
МАТЕМАТИЧЕСКОЙ СТАТИСТИКЕ
В данном разделе приведены задания по статистической обработке и анализу одномерных (задача
№10) и двумерных (задача №11) случайных величин.
ЗАДАЧА 10.
По выборке одномерной случайной величины:
- получить вариационный ряд;
- построить на масштабно-координатной бумаге формата А4 график эмпирической функции
распределения F*(x);
- построить гистограмму равноинтервальным способом;
- построить гистограмму равновероятностным способом;
- вычислить оценки математического ожидания и дисперсии;
- выдвинуть гипотезу о законе распределения случайной величины и проверить ее при помощи
критерия согласия χ2 и критерия Колмогорова (α = 0,05).
№10,11
Вариационный ряд
-3,61
-3,07
-2,91
-2,83
-2,78
-2,41
-2,35
-2,15
-2,03
-1,99
-1,93
-1,82
-1,75
-1,71
-1,39
-1,36
-1,27
-1,23
-1,22
-0,96
-0,95
-0,9
-0,86
-0,71
-0,7
-0,69
-0,68
-0,66
-0,64
-0,61
-0,52
-0,42
-0,33
-0,32
-0,21
-0,19
-0,19
-0,19
-0,14
-0,1
-0,09
-0,08
-0,04
-0,03
0,05
0,08
0,12
0,12
0,21
0,24
0,24
0,31
0,36
0,39
0,40
0,42
0,44
0,44
0,45
0,46
0,50
0,51
0,54
0,54
0,55
0,57
0,61
0,67
0,68
0,73
0,75
0,76
0,85
0,86
0,87
0,93
1,09
1,11
1,19
1,19
1,24
1,33
1,41
1,47
1,48
1,51
1,61
1,62
1,62
1,77
1,99
2,01
2,05
2,10
2,13
2,22
2,28
2,45
2,73
3,12
Эмпирическая функция распределения
По формуле
0, x x1,
i
F * ( x) p* ( X x) , xi x xi 1
n
1, x x .
n
распределения
построим график эмпирической функции
F * ( x) . Так как F * ( x) является неубывающей функцией и все ступеньки графика F * ( x)
имеют одинаковую величину 1/n (или ей кратны – для одинаковых значений), то таблицу значений
эмпирической функции распределения F*(x) можно не вычислять, а построить ее график непосредственно
по и вариационному ряду, начиная с его первого значения
Количество интервалов M, необходимое для построения гистограмм, определим
по объему выборки ( см. формулу (10.2)):
M n 100 10.
Для равноинтервальной гистограммы величины hj, Aj, Bj, рассчитаем по формуле
x x
и заполним все колонки
h j h n 1 , j A j x1 ( j 1)h, j 2, M
M
интервального статистического ряда :
Шаг интервала
h=
xmax xmin
10
h=(3,12+3,61)/10=0.673
i
f *i
i
Bi
hi
-3,610
-2,937
0,673
2
0,02
0,030
0,02
-2,937
-2,264
0,673
5
0,05
0,074
0,07
-2,264
-1,591
0,673
7
0,07
0,104
0,14
-1,591
-0,918
0,673
7
0,07
0,104
0,21
-0,918
-0,245
0,673
13
0,13
0,193
0,34
Ai
pi *
nhi
px
-0,245
0,428
0,673
22
0,22
0,327
0,56
0,428
1,101
0,673
21
0,21
0,312
0,77
1,101
1,774
0,673
13
0,13
0,193
0,9
1,774
2,447
0,673
7
0,07
0,104
0,97
2,447
3,120
0,673
3
0,03
0,045
1
Гистограмма равноинтервальным способом
Гистограмма равновероятностным способом
Ai
Bi
-3,610
-2,937
-2,264
-1,591
-0,918
-0,245
0,428
1,101
1,774
2,447
-2,937
-2,264
-1,591
-0,918
-0,245
0,428
1,101
1,774
2,447
3,120
hi
i
pi *
1,68
0,98
0,43
0,43
0,33
0,26
0,25
0,49
0,75
1,13
10
10
10
10
10
10
10
10
10
10
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
f *i
i
nhi
0,060
0,102
0,233
0,233
0,303
0,385
0,400
0,204
0,133
0,088
Вычислим точечную оценку математического ожидания по формуле:
m*X x
1 n
xi 0.0735 .
n i 1
Вычислим точечную оценку дисперсии по формуле:
D*X S02
1 n 2
n
xi
x 2 1.93 .
n 1 i 1
n 1
Построим доверительный интервал для математического ожидания с
S
S
надежностью γ = 0,95 по формуле I γ (mX ) x zγ 0 ; x zγ 0 , .
n
n
γ
= 0,475, и
2
определим значение аргумента, ему соответствующее: z0,95 arg (0,475) 1,96 .
Для этого в таблице функции Лапласа найдем значение, равное
S0
0,272 и получим доверительный интервал для
n
математического ожидания:
Затем вычислим
z0,95
I 0,95 (mX ) 0.199;0.346 .
Построим доверительный интервал для дисперсии с надежностью γ = 0,95 по
2 2 2
2 2
S0 ; S0 z γ
S0 .
формуле I γ ( DX ) S02 zγ
n
1
n
1
2
S02 0.538 и получим доверительный интервал для
n 1
Вычислим z0,95
дисперсии:
I 0,95 ( Dx ) 1.392;2.467 .
По виду гистограммы выдвинем гипотезу о нормальном распределении СВХ. Проверим гипотезу о
нормальном распределении СВХ при помощи критерия χ2
Н0: F(x)=F0(x), f ( x) f 0 ( x)
Н1: F(x)≠F0(x), f ( x) f 0 ( x)
Где F0(x), f 0 ( x) – теоретическая функция и плотность распределения
f 0 ( x)
1
X 2
e
x a 2
2X2
xa
X
, F0 ( x) 0.5 Ф
Где
a X 0.0735
X s 1.930 1.389
1
f 0 ( x)
e
1.389 2
χ2= n
( pi pi* )2
p
i
x 0.07352
21.930
B X
pi F0 ( Bi ) F0 ( Ai ) Ф i
S
Ai
Bi
-2,937
-2,264
-1,591
-0,918
-0,245
0,428
1,101
1,774
2,447
-2,937
-2,264
-1,591
-0,918
-0,245
0,428
1,101
1,774
2,447
x 0.0735
1.389
, F0 ( x) 0.5 Ф
F0 ( Ai )
Ai X
Ф
S
F0 ( Bi )
0
0,0139
0,0433
0,1100
0,2297
0,4001
0,5924
0,7643
0,8863
0,9548
0,0139
0,0433
0,1100
0,2297
0,4001
0,5924
0,7643
0,8863
0,9548
1
сумма
pi F0 ( Bi ) F0 ( Ai )
0,0139
0,0294
0,0667
0,1197
0,1704
0,1923
0,1720
0,1220
0,0686
0,0452
1
pi*
( pi pi* )2
pi
0,02
0,05
0,07
0,07
0,13
0,22
0,21
0,13
0,07
0,03
1
0,00267
0,01437
0,00017
0,02064
0,00957
0,00400
0,00841
0,00053
0,00003
0,00509
0,06548
χ2=100*0.065=6,5
По таблице найдем критическое значение критерия χ2кр(7;0,05)=14,1, так как χ2кр> χ2 то гипотеза о
нормальном распределении СВ Х принимается.
Проверим гипотезу о нормальном распределении СВ Х при помощи критерия Колмогорова
Н0: F(x)=F0(x)
Н1: F(x)≠F0(x)
Где F0(x)– теоретическая функция распределения
n
Z max F * ( xi ) F0 ( xi ) 0,06
i 1
Вычислим значение критерия Колмогорова по формуле:
n Z 100 0,06 0,6.
Из таблицы Колмогорова по заданному уровню значимости =0,05 выбираем
критическое значение λ γ λ1-α λ0,95 1,36.
Так как λ 0,6 λ0,95 1,36 , то гипотезу H 0 о нормальном законе распределения
отвергать нет основания.
ЗАДАЧА 11.
По выборке двухмерной случайной величины:
- вычислить оценку коэффициента корреляции;
- вычислить параметры линии регрессии a0 и a1;
- построить диаграмму рассеивания и линию регрессии
№10
Состоятельная оценка коэффициента корреляции
*
RXY
n
XY XY
n
1
s X sY
Расчетная таблица
X
Y
2,74
0,86
1,68
-0,48
-0,17
1,25
0,76
0,71
1,38
2,75
2,63
0,04
2,06
2,57
2,42
1,53
3,7
0,75
0,23
1,06
2,36
2,53
3,15
0,8
3,03
0,65
0,69
-0,31
X*Y
X2
8,0556
2,94
3,3024
3,84
4,4016
2,62
0,03 -0,0144
0,0799
-0,47
2,025
1,62
0,76
1
-1,03 -0,7313
3,9054
2,83
3,63
1,32
8,153
3,1
0,1856
4,64
0,309
0,15
4,14 10,6398
7,8892
3,26
3,7944
2,48
3,626
0,98
1,2525
1,67
0,8855
3,85
0,4664
0,44
7,5048
3,18
4,1998
1,66
11,088
3,52
0,704
0,88
4,9995
1,65
1,5665
2,41
0,069
0,1
0,53 -0,1643
Y2
7,5076
0,7396
2,8224
0,2304
0,0289
1,5625
0,5776
0,5041
1,9044
7,5625
6,9169
0,0016
4,2436
6,6049
5,8564
2,3409
13,69
0,5625
0,0529
1,1236
5,5696
6,4009
9,9225
0,64
9,1809
0,4225
0,4761
0,0961
8,6436
14,7456
6,8644
0,0009
0,2209
2,6244
1
1,0609
8,0089
1,7424
9,61
21,5296
0,0225
17,1396
10,6276
6,1504
0,9604
2,7889
14,8225
0,1936
10,1124
2,7556
12,3904
0,7744
2,7225
5,8081
0,01
0,2809
0,87
2,56
2,68
2,54
1,4
1,23
3,06
4,18
3,61
4,09
1,96
-0,21
0,15
0,27
0,68
0,18
3,64
1,03
-0,39
3,63
2,08
4,07
84,68
1,6936
сумма
среднее
2,88
3,16
3,36
2,17
1,51
2,47
3,52
4,22
0,99
1,84
1,16
2,47
2,27
2,51
0,64
0,7
1,61
2,25
4,15
3,92
3,46
1,27
105,87
2,1174
2,5056
8,0896
9,0048
5,5118
2,114
3,0381
10,7712
17,6396
3,5739
7,5256
2,2736
-0,5187
0,3405
0,6777
0,4352
0,126
5,8604
2,3175
-1,6185
14,2296
7,1968
5,1689
198,85
3,9769
0,7569
6,5536
7,1824
6,4516
1,96
1,5129
9,3636
17,4724
13,0321
16,7281
3,8416
0,0441
0,0225
0,0729
0,4624
0,0324
13,2496
1,0609
0,1521
13,1769
4,3264
16,5649
231,56
4,6312
X =1,6936
Y =2,1174
XY =93,9769
X 2 =4,6312
Y 2 =6,2893
SX
n
X 2 ( X )2
n 1
sY
n
Y 2 (Y )2
n 1
SY
50
6.2893 (2.1174) 2 =1,357
50 1
Sx
50
4.6312 (1.6936)2 =1,341
50 1
дисперсия
S x2 1,799
S y2 =1,843
Состоятельная оценка коэффициента корреляции
8,2944
9,9856
11,2896
4,7089
2,2801
6,1009
12,3904
17,8084
0,9801
3,3856
1,3456
6,1009
5,1529
6,3001
0,4096
0,49
2,5921
5,0625
17,2225
15,3664
11,9716
1,6129
314,46
6,2893
*
RXY
93.9769 1.6936 2.1174
1.357 1.341
50
50 1 =0,219
Уравнение регрессии имеет вид
*
y Y RXY
Sy
SX
(x X )
Y-2,1174=0,219*(1,357/1,341)(x-1,6936)
y=0,222x+1,742
a0=0,222
a1=1,742
проверим значимость коэффициента корреляции, при помощи критерия t
*
H0: RXY
=0
*
H1: RXY
0
t=
t=
*
RXY
n2
* 2
1 RXY
0.222 50 2
1 0.2222
=1,56
по таблице найдем критическое значение Tкр(0,05;48)=2,02, так как |t|<Tкр то коэффициент корреляции
незначим.
Доверительный интервал для коэффициента корреляции
e 2 a 1 e 2b 1
I RXY 2 a ; 2b
e 1 e 1
1 RXY
1 RXY
Где a 0.5 ln
z
1 RXY
b 0.5 ln
n3
1 RXY
z
n3
Для 0, 95 z 1,96
1,96
1 0.222
a 0.5 ln
-0.0632
50 3
1 0.222
1,96
1 0.222
b 0.5 ln
0.5086
50 3
1 0.222
e 2 0.0632 1 e 2 0.5086 1
I RXY 2 0.0632 ; 2 0.5086 0.063;0.469
1 e
1
e
z arcФ
2