КР по ТФКП

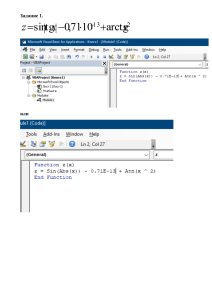
Тренировочный вариант семестровой контрольной работы №2 по модулю
«Основы ТФКП» (на 45 мин.)
Задание 1-а. Вычислить значение функции f ( z ) в точке z0 :
1 i 3
; 2) f ( z )  z1i , z0  3  4i .
2
1 
4
4 
 
 i

Ответ: 1)   2 k   ln 2  3 ; 2) 5earctg (4/3)2 k cos  ln 5  arctg   i sin  ln 5  arctg   .
2 2
3
3 
 2

 
1) f ( z )  Arctgz, z0 


Задание 1-б. Найти значение модуля функции w  f ( z )  sin z в точке z    i ln(2  5) .
Ответ: 2.
Задание 1-в. Найти все корни уравнения: 1) sin z  cos z  2; 2) 2chz  shz  i .

1
1
Ответ: 1) z   2k  i ln( 2  1); 2) z  (2k  ) i, z   ln 3  (2k  ) i.
4
2
2
Задание 2. Найти аналитическую функцию f ( z )  u  iv по заданной действительной или
y
мнимой части: 1) u  x 2  y 2  5x  y  2
;
2) v  ln( x 2  y 2 )  x  2 y.
Ответ: 1)
2
x y
i
f ( z )  z 2  (5  i ) z   Ci ; 2) f ( z )  2i ln z  (2  i ) z  C . Всюду С - произвольная действительная
z
постоянная.
Задание 3-а. Вычислить интегралы: 1)  e z dz , где L – отрезок прямой y   x , соединяющий
L
отрезки z1  0 и z2    i ; 2)
2 i
 (3z
2
 2 z )dz; 3)
1i
chiz
z  4z  3
z 2

2

Ответ: 1) (e  1)i ; 2) 7  19i; 3)  i cos1.
Задание 3-б. Вычислить интегралы: 1)
3)
2
sh z
dz; 2)
z3
z 1

chei z
2
Ответ:
1)
;
2)
0;
3)
sh1.
dz
.
2 i
3
2

z

4
z
2
z  2 3
Задание 3-в
Ответы:
1
z
e
dz;
( z  4)2
z  2 1

2