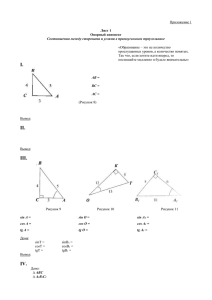
АСК в составе ГУ ВПО «БРУ» Техническая механика Контрольная работа №1 Вариант №0 Игнатенкова С.В. Учащегося(щейся) 1 курса специальности 1Сз-2к группы Промышленное и гражданское строительство Шифр учащегося(щейся) 16 1Сз-2к/ПГС 010 Задача 1 Определить усилия в стержнях кронштейна от приложенной внешней силы. Задачу выполнить аналитическим и графическим способами. Трением пренебречь. Исходные данные приведены на рисунке 1 и в таблице 1. Рисунок 1 – Схемы кронштейна Таблица 1 - Исходные данные для задачи 1 Последняя цифра F, кН 0 15 α Углы, град. β γ 40 100 60 Решение АВС 180о 40о 90о 50о 1 Выбираем точку, равновесие которой будем рассматривать − точка В. 2 Освобождаем узел В от связей и заменяем их реакциями, предполагая, что стержни растянуты, т. е. усилия направлены от узла. Аналитический способ решения 3 Выбираем расположение осей координат так, чтобы одна из осей прошла через неизвестное усилие (N1) (рисунок 2). Рисунок 2 4 Составляем уравнения равновесия. X 0 ; Y 0 ; N1 N 2 cos 50o F cos 70o 0 ; N 2 cos 40o F cos 20o 0 ; F cos 20o 15 0,94 N2 18,31 кН (сжатие); cos 40o 0, 77 N1 N 2 cos 50o F cos 70o 18,31 0, 64 15 0,34 16,81 кН (растяжение). Графический способ решения 1 Выбираем масштаб сил: 1 см = 10 кН. 2 Строим замкнутый силовой многоугольник (построение начинается с известной силы) (рисунок 3). Измеряем полученные отрезки и умножаем их на масштаб. N1 = 1,8 см ∙ 10 = 18 кН Направление силы совпадает с первоначальным, значит, стержень 1 растягивается. N2 = 1,68 см∙10 = 16,81 кН Рисунок 3 Направление силы не совпадает с первоначальным, значит, стержень 2 сжимается. Ответ: стержень 1 − растянут (N1 = 18,31 кН), стержень 2 − сжат (N2 = − 16,81 кН). Задача 2 Определить опорные реакции консольной балки. Исходные данные приведены на рисунке 1 и в таблице 1. Рисунок 1 – Схемы нагружения консольной балки Таблица 1 - Исходные данные для задачи 2 Последняя цифра F, кН q, кН/м m, кН·м а1, м а2, м а3, м α 0 15 20 25 1,8 1,0 2,2 80 Решение: Рисунок 2 – схема решения задачи 1. Согласно схеме решения задач (рисунок 2) статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки. 2. На балку наложена связь в точке A (слева) типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (HA, RA, MA). 3. Определим реакции опор в соответствии с уравнениями равновесия балки: ΣFx = 0, ΣFy = 0, ΣMA = 0. ΣFx = 0: HA + P1*cos(80) = 0 ΣFy = 0: RA - q1*1 + P1*sin(80) = 0; ΣMA = 0: MA - q1*1*(1.8+1/2) + M1 + 5*P1*sin(80) = 0; 4. Решаем полученную систему уравнений, находим неизвестные : HA = - P1*cos(80) = - 15*0.1736 = -2.60 (кН), так как реакция отрицательна, на расчетной схеме направим ее в противоположную сторону. RA = q1*1 - P1*sin(80) = 20*1 - 15*sin(80) = 5.23 (кН) MA = q1*1*(1.8+1/2) - M1 - 5*P1*sin(80) = 20*1*(1.8 + 1/2) - 25 - 5*15*sin(80) = -52.86 (кН*м), так как момент отрицателен, на расчетной схеме направим его в противоположную сторону. 5. Сделаем проверку, составив дополнительное моментное уравнение отоносительно свободного конца балки: - 5*RA - MA + q1*1*(2.2+1/2) + M1 - 0*P1*sin(80) = - 5*5.23 - 52.86 + 20*1*(2.2+1/2) + 25.00 - 0*15*sin(80) = 0 Задача 3 Определить опорные реакции двухопорной балки. Исходные данные приведены на рисунке 1 и в таблице 1. Рисунок 1 – Схемы нагружения двухопорной балки Таблица 1 - Исходные данные для задачи 3 Последняя цифра F, кН 0 25 q, кН/м m, кН·м 30 15 а1, м а2, м а3, м а4, м α 1,6 1,0 2,2 1,8 60 Решение Рисунок 2 – схема решения задачи 1. Согласно схеме решения задач статики определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки. ΣFx = 0: - P1*cos(60) + HB = 0 ΣMA = 0: Найдем сумму моментов относительно шарнирно-подвижной опоры в точке A: M1 - q1*1*(1/2) - P1*sin(60)*1 + RB*3.2 = 0 ΣMB = 0: Найдем сумму моментов относительно шарнирно-неподвижной опоры в точке B: M1 - RA*3.2 + q1*1*(3.2 - 1/2) + P1*sin(60)*2.2 = 0 2. Решаем полученную систему уравнений, находим неизвестные : HB = P1*cos(60) = 25*0.5000 = 12.50 (кН) 3. Вычислим реакцию шарнирно-неподвижной опоры в точке B RB = ( - M1 + q1*1*(1/2) + P1*sin(60)*1) / 3.2 = ( - 15 + 30*1*(1/2) + 25*sin(60)*1) / 3.2 = 6.77 (кН) 4. Вычислим реакцию шарнирно-подвижной опоры в точке A RA = ( M1 + q1*1*(3.2 - 1/2) + P1*sin(60)*2.2) / 3.2 = ( 15 + 30*1*(3.2 - 1/2) + 25*sin(60)*2.2) / 3.2 = 44.88 (кН) 5. Выполним проверку ΣFy = 0: RA - q1*1 - P1*sin(60) + RB = 44.88 30*1 - 25*sin(60) + 6.77 = 0 Задача 4 Определить координаты центра тяжести поперечного сечения геометрической формы (рисунок 1). Построить в выбранном масштабе (таблица 1). Рисунок 1 Таблица 1 Последняя цифра 0 а, см b, см h1,см h2, см h3, см 40 30 18 27 33 Решение 1 Сложную фигуру разбиваем на сумму простых фигур: прямоугольник площадью А1, прямоугольник площадью А2, трапеция площадью А3 (рисунок 2). Рисунок 2 2 Заданное поперечное сечение имеет вертикальную ось симметрии (ось У) и центр тяжести лежит на этой оси. Следовательно, относительно системы координат ХУ координата центра тяжести всего сечения хс = 0, требуется определить координату ус по формуле(1): yc Sx A i yi , A Ai (1) где Sx − статический момент поперечного сечения; А − площадь поперечного сечения; Ai − площадь i-ой фигуры; yi − координата центра тяжести i-ой фигуры. 3 Находим площадь каждой фигуры и общую площадь поперечного сечения. А1 = b ∙h3 = 30∙33 = 990 см2; А2 = (a+b+a)∙h2 = (40+30+40)∙27= 2970 см2; 1 1 A3 ((a b a) b) h1 ((40 30 40) 30) 18 1260 см 2 ; 2 2 A Ai A1 A2 A3 990 2970 1260 5220 см2 . 4 Находим координаты центров тяжести каждой простой фигуры относительно оси Х. Для фигуры 1 (прямоугольник): y1 h1 h2 h3 33 18 27 61,5см ; 2 2 Для фигуры 2 (прямоугольник): y2 h1 h2 18 27 22,5 см ; 2 2 Для фигуры 3 (трапеция): y3 h1 (2 b (2 a b)) 18 (2 30 (2 40 30)) 7, 28 см . 3 (b (2 a b)) 3 (30 (2 40 30)) 5 Вычисляем координату центра тяжести поперечного сечения: yc S x Ai yi 990 61,5 2970 22,5 1260 7, 28 26, 22 см . A 5220 Ai Ответ: хс = 0, ус = 26,22 см. Задача 5 Определить координаты центра тяжести сечения, составленного из стандартных профилей проката. Исходные данные приведены на рисунке 1 и в таблице 1. Рисунок 1 – Схемы сечений из профилей проката Таблица 5 – Исходные данные для задачи 5 Последняя цифра 0 Номер профиля для фигуры 1 22 2 27 Решение: 1 − Швеллер № 22; 2 − Двутавр № 27 1 Вычерчиваем заданное поперечное сечение (рисунок 2). Размеры фигур берутся из таблиц сортамента (ГОСТ 8239-89, ГОСТ 8240-97). Швеллер № 22: h = 22 см, b = 8,2 см, d = 0,54 см, t = 0,95 см, z0 = 2,21 см, А = 26,7 см2. Двутавр № 27: h = 27 см, b = 12,5 см, d = 0,6 см, t = 0,98 см, А = 40,2 см2. Рисунок 2 2 Заданное поперечное сечение имеет вертикальную ось симметрии (ось У) и центр тяжести лежит на этой оси. Следовательно, относительно системы координат ХУ координата центра тяжести всего сечения хс = 0, требуется определить координату ус по формуле (1). 3 Находим общую площадь поперечного сечения. A Ai A1 A2 26,7 40, 2 66,9 см2 . 4 Находим координаты центров тяжести фигур относительно оси Х. Для фигуры 1 (швеллер): y1 hдв dшв z0 27 0,54 2, 21 25,33 см ; Для фигуры 2 (двутавр): y2 hдв 27 13,5см . 2 2 5 Вычисляем координату центра тяжести поперечного сечения: yc A y A i i i 26,7 25,33 40, 2 13,5 18, 22 см . 66,9 Ответ: хс = 0, ус = 18,22 см. (1) Используемая литература: 1 Сетков, В. И. Сборник по технической механике: Учеб. пособие для техникумов. – Москва : Стройиздат, 1982. – 176 с. 2 Бычков, Д. В., Миров М. О. Теоретическая механика : Учеб. для техникумов. Изд. 4-е, испр. – Москва : Высшая школа, 1976. - 240 с. 3 Михайлов, А. М. Сопротивление материалов: Учеб. для техникумов.– Москва : Стройиздат, 1989. – 352 с.