Пример решения задачи 1 Тело движется из точки А по участку

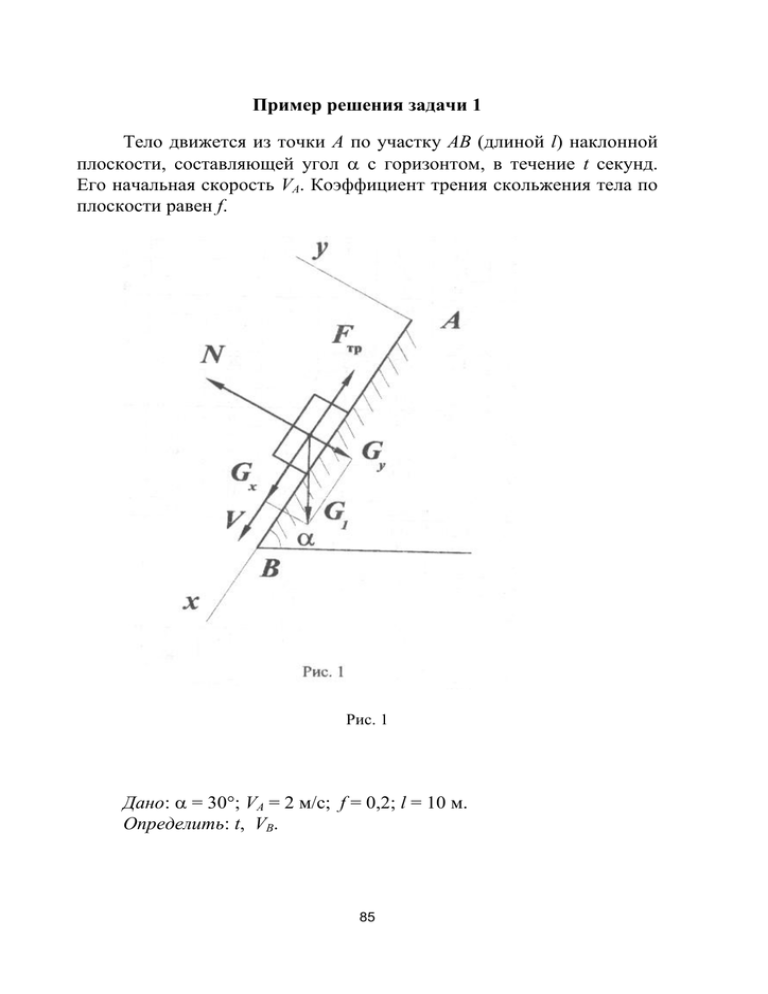
Пример решения задачи 1
Тело движется из точки А по участку АВ (длиной l) наклонной
плоскости, составляющей угол  с горизонтом, в течение t секунд.
Его начальная скорость VA. Коэффициент трения скольжения тела по
плоскости равен f.
Рис. 1
Дано:  = 30; VA = 2 м/с; f = 0,2; l = 10 м.
Определить: t, VВ.
85
Решение
Рассмотрим движение тела на участке АВ, принимая тело за ма
териальную точку, покажем
действующие на него силы

 тяжести G ,
нормальную реакцию N и силу трения скольжения Fтp .
Составим дифференциальные уравнения движения тела на участке АВ:
mx   Fix ,

my   Fiy ,
где m – масса точки; x, y – ускорения точки в проекциях на оси х, у;
 Fiх ,  Fiу – сумма проекций всех сил на оси х, у.
Для данной задачи дифференциальные уравнения будут записаны так:
mx  G sin α  Fтp,

my  N  G cosα.
Так как движение тела происходит только вдоль оси х, а вдоль
оси у движения нет, то y  0 .
Следовательно, 0 = N – G cos , N = G cos  = mg cos . Тогда
mx  G sin α  fN ,
mx  mg sin α  fmg cos α ,
x  g sin α  fg cos α ,
x  3,2.
Получили дифференциальное уравнение второго порядка с разделяющими переменными
dx
 3,2; dx  3,2dt ;
dt
 dx  3,2 dt ;
x  3,2t  C1 .
86
(1)