Министерство образования и науки
Республики Казахстан
Карагандинский государственный технический
университет
Кафедра «Энергетические системы»
КОНТРОЛЬНАЯ
РАБОТА
Дисциплина Ele 2211 «Электротехника»
Специальность 5В072400 – «Технологические машины и
оборудование »
Факультет заочно-дистанционного обучения
Руководитель
(фамилия инициалы)
(подпись)
(дата)
Ст
ГМ-17у 17/12удент
196
(группа)
Огай А.В.
(фамилия инициалы)
(подпись)
2018
( дата)
Контрольная работа № 1
Расчет электрической цепи постоянного тока с несколькими источниками электрической
энергии
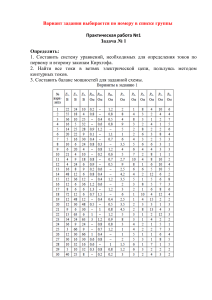
Для электрической цепи, схемы которых изображены на рисунке 1.1. по заданным в
таблице 1 сопротивлениям и ЭДС, выполнить следующее:
1.Рассчитать токи ветвей, пользуясь методом контурных токов.
2.Проверить правильность решения на основании законов Кирхгофа.
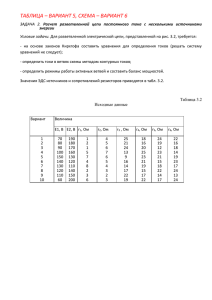
Таблица 1
Номер
варианта
Номер
схемы
R1,
Oм
R2,
Oм
R3,Oм
R4, Oм
R5, Oм
R6, Ом
E1, B
E2, B
E3, B
15
1.1
2
3
8
5
7
8
12
6
40
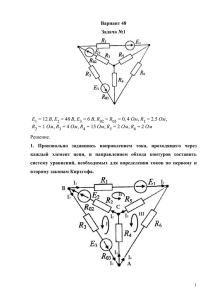
Схема 1.1.
Общий план составления уравнений
1 – Выбор независимых контуров и направления контурных токов в
них.
2 – Определение собственных и общих сопротивлений контуров
3 – Составление уравнений и нахождение контурных токов
4 – Выбор направления действительных токов.
5 – Нахождение действительных токов.
2
Дано:
Е1 = 12 В (вольт)
Е2 = 6 В (вольт)
Е3 = 40 В (вольт)
R1 = 2 Oм
R2 = 3 Oм
R3 = 8 Oм
R4 = 5 Oм
R5 = 7 Oм
R6 = 8 Oм
Найти: I1-6 - ?
Решение:
1. Выделяем три контура, а затем указываем направление контурных
токов Iк1,Iк2,Iк3. Мы выберем направление по часовой
стрелке.
3
Для заданной цепи
у 4 – число узлов; в 6 – число ветвей.
Применяем метод контурных токов
Система уравнений для контурных токов по второму закону Кирхгофа
𝐼𝐾1 (𝑅1 + 𝑅3 + 𝑅5 ) − 𝐼𝐾2 ∙ 𝑅3 − 𝐼𝐾3 ∙ 𝑅5 = 𝐸1 − 𝐸3
{𝐼𝐾2 (𝑅2 + 𝑅6 + 𝑅3 ) − 𝐼𝐾1 ∙ 𝑅3 − 𝐼𝐾3 ∙ 𝑅6 = 𝐸2 + 𝐸3
𝐼𝐾3 (𝑅6 + 𝑅4 + 𝑅5 ) − 𝐼𝐾2 ∙ 𝑅6 − 𝐼𝐾1 ∙ 𝑅5 = 0
4
𝐼𝐾1 (2 + 8 + 7) − 𝐼𝐾2 ∙ 8 − 𝐼𝐾3 ∙ 7 = 12 − 40
{ 𝐼𝐾2 (3 + 8 + 8) − 𝐼𝐾1 ∙ 8 − 𝐼𝐾3 ∙ 8 = 6 + 40
𝐼𝐾3 (8 + 5 + 7) − 𝐼𝐾2 ∙ 8 − 𝐼𝐾1 ∙ 7 = 0
𝐼𝐾1 ∙ 17 − 𝐼𝐾2 ∙ 8 − 𝐼𝐾3 ∙ 7 = −28
{ 𝐼𝐾2 ∙ 19 − 𝐼𝐾1 ∙ 8 − 𝐼𝐾3 ∙ 8 = 46
𝐼𝐾3 ∙ 20 − 𝐼𝐾2 ∙ 8 − 𝐼𝐾1 ∙ 7 = 0
Решение системы уравнений методом определителей
17 −8 −7
∆ | −8 19 −8 | = 2265
−7 −8 −20
−28
∆1 | 46
0
−8
19
−8
−7
−8 | = 1088
−20
17
∆2 | −8
−7
−28
46
0
−7
−8 | = 7338
−20
17
∆3 | −8
−7
−8
19
−8
−28
46 | = 3316
0
Контурные токи
IK1=
IK2=
∆1
∆
∆2
∆
= 1088
= 0,480 A
2265
7338
= 2265 = 3,240 A
5
IK3=
∆3
∆
=
3316
2265
= 1,464 A
Токи ветвей:
I1 = IК1 = 0,480 A
I2 = IК2 = 3,240 A
I3= IК1 – IК2= 0,480 - 3,240 = - 2,76 A
I4 = IК4 = 1,464 A;
I5 = – IК1-К3 = 0,480 - 1,464 =0,984 А
I6 = IК2 – IК3= 3,240 - 1,464 = 1,776A
Выполним проверку, используя первый закон Кирхгофа:
Для уз. a = I1 - I2- I3 = 0
Для уз. A = 0,480 - 3,240+2,76 = 0
Для уз. b = I5 + I4- I1 = 0
Для уз. b = -0,984 + 1,464 - 0,480 = 0
Для уз. d = I2 – I6 – I4 = 0
Для уз. d = 3,240 – 1,776 – 1,464 = 0
Ответ: I1 = 0,480 A; I2 = 3,240 A; I3= - 2,76 A; I4 = 1,464 A; I5 =0,984 А;
I6 = 1,776A.
6